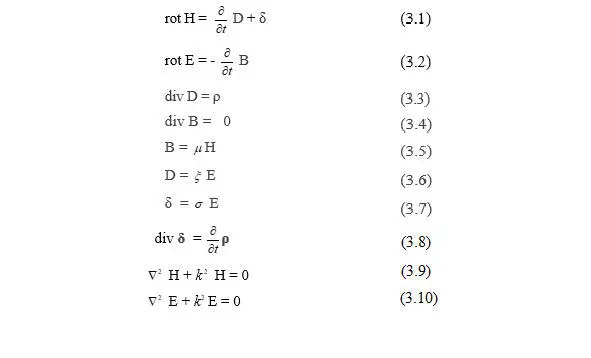Математическая модель электромагнитного поля представляет систему уравнений электромагнитного поля в полном виде или систему уравнений Максвелла [4].
Электромагнитное поле характеризуются следующими векторными величинами: E и H – векторы напряженности электрического и магнитного полей, D и B – векторы электрической и магнитной индукции, I и Im – плотность токов электрической и магнитной проводимости, ρ и ρ m – плотность электрических и магнитных зарядов.
Дифференциальная форма системы уравнений выглядит (3.1 – 3.7), где – магнитная проницаемость, – диэлектрическая проницаемость, – удельная проводимость
Эти уравнения будут исходными при рассмотрение переменных электромагнитных полей и процессов.
Первое уравнение Максвелла. является дифференциальной формулировкой закона полного тока. Физический смысл 1-го уравнения Максвелла: источниками вихревых магнитных полей являются токи проводимости и токи смещения.
Величина δв правой части (3.1) есть плотность тока проводимости. Это вектор, указывающий направление движения зарядов.
Законы электромагнетизма – это законы макроскопических процессов, в которых усредняется действие огромных количеств элементарных частиц материи. С точки зрения этих законов, среда представляется сплошной.
Второе уравнение Максвелла (3.2) является дифференциальной формулировкой закона электромагнитной индукции и выражает скорость изменения магнитной индукции В через пространственную производную (rot) напряженности электрического поля Е.
Физический смысл: вихревое электрическое поле создается переменным магнитным полем
Третье уравнение Максвелла является дифференциальной формулировкой теоремы Гаусса для электрических полей. Физический смысл: источниками электрического поля (векторов Е и D) являются заряды с плотностью ρ. Дифференциальные уравнения (3.3) показывает, что расходимость электрической индукции равна объемной плотности заряда.
Четвертое уравнение Максвелла является дифференциальной формулировкой теоремы Гаусса для магнитных полей. Физический смысл. Дивергенция вектора В в любой точке пространства равняется нулю, т.е. – источников нет (магнитные заряды в природе отсутствуют). Нет ни стыков, ни источников. Линии магнитной индукции непрерывны.
Из уравнений (3.1) и (3.3) можно прийти к уравнению (3.8).
Это уравнение непрерывности. Закон сохранения заряда.
Уравнения (3.5), (3.6), (3.7) характеризуют связь векторов поля с материальной средой.
Установим волновой характер ЭМП. При распространении ЭМП с конечной скоростью происходит запаздывание его по фазе, результатом чего является волновой характер распространения. Можно записать первые два уравнения Максвелла в комплексной форме и заменить в них индукции B и D напряженностями rot E и rot H и ввести функцию комплексной диэлектрической проницаемости проводящей среды при монохроматическом поле. Затем получится полная система уравнений монохроматического ЭМП с комплексными проницаемостью и напряженностями E и H. Волновой характер ЭМП этого гармонического во времени процесса в области без источников получается, если исключить вектор E или вектор H из в уравнениях (3.1) и (3.2), применив оператор rot и учитывая, что расходимость (div) вектора H = 0.
Для однородной непроводящей среды волновое уравнение переходит в уравнение Гельмголца, которое запишется в уравнения (3.9 – 3.10), где k = ω εμ – волновое число.
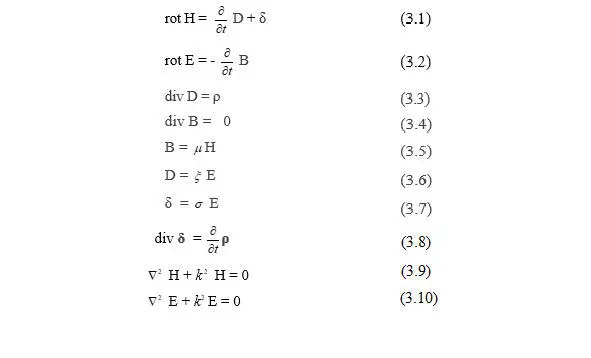
Об аналогии описания физических полей
Из рассмотренных математических моделей физических полей микромира видно, что гравитационное, акустическое и электромагнитное поля описываются при определенных условиях волновыми уравнениями (1.9, 2.7, 2.8, 3.9, 3.10). Мы имеем ситуацию, когда различные физические явления (поля) описываются аналогичными дифференциальными и другими уравнениями. То есть между физическими явлениями существует аналогия, которая основывается на сходстве уравнений, лежащих в основе описания данных физических явлений
Аналогия ЭМП и акустического поля.
Например, акустические волны описываются уравнениями Гельмгольца (2.8). Электромагнитные волны описываются уравнениями Максвелла, которые после соответствующих преобразований также переходят в уравнения Гельмгольца для однородной среды (3.9). Т.е. в двумерном случае уравнения Максвелла сводятся к двум независимым уравнениям для векторов напряженности электрического и магнитного полей (4.1 – 4.2).
Читать дальше