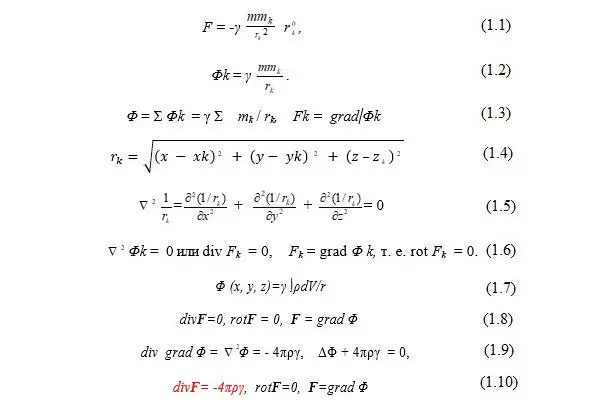Геннадий Вильдяйкин - Исследование и оценка параметров сигналов в распределенных информационных системах. Для студентов технических специальностей

ГАП-ГАП. За счет нелинейности жидкой среды формируются поля и спектры частот, которые содержат сведения о технических средствах. Например, кавитационный спектр, модуляционный спектр и др.

АПВ-АПВ. Формирование и снятие данных за счет взаимодействия акустических волн низких и высоких частот на нелинейных структурах.

Математическая модель физических полей макромира

Математическая модель охватывает класс неопределяемых абстрактных, символических математических объектов, таких как числа или векторы, и отношения между этими объектами.

Под математической моделью понимают количественную формализацию абстрактных представлений об изучаемой системе. Математическая модель это формальное описание системы с помощью математических средств, дифференциальных, интегральных, разностных, алгебраических уравнений, а также неравенств, множеств и т. д.

Рассмотрим математическую модель физических полей макромира (гравитационного, электромагнитного, акустического) (Рис.1), которая характеризует информацию.

Математическую модель гравитационного поля представим дифференциальным уравнением гравитационного поля в ньютоновской механике [2].Такое уравнение получаются переходом от закона всемирного тяготения Ньютона, где сила взаимного притяжения двух тел, которые могут быть приняты за материальные точки, прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними, к дифференциальным уравнениям в теории ньютоновского потенциала.

Итак, имеются две материальные точки с массами m и m они притягиваются друг к другу по закону Ньютона и на точку m со стороны точки m действует сила (1.1), где r k – расстояние между точками т и m k, γ – гравитационная постоянная, r – единичный вектор направления от m к m .

Потенциальный характер сил тяготения т. е. Fk = grad Φk, позволяет ввести скалярную характеристику гравитационного поля – потенциал, который для двух материальных точек (1.2).

Если и пространстве имеется n материальных точек с массами m (k = 1, 2,.. п) и рассматривается их влияние на одну материальную точку массы m = 1 , которая может быть помещена в разные точки пространства (пробная масса), то со стороны всех точек m k на пробную массу m = 1 будет действовать сила F = Σ Fk и ее потенциал (1.3).

Распределение масс m k создает в пространстве гравитационное поле с потенциалом Φ , которое можно обнаружить с помощью пробной массы, помещенной в рассматриваемую точку пространства. Напишем дифференциальное уравнение, которому должен удовлетворять потенциал сил тяготения Φ. [2] Рассмотрим функцию 1 /, где (1.4) – расстояние между точкой х, у, z, в которой помещена пробная масса, и точкой x k, y k, z к, в которой находится k-тая масса, создающая гравитационное поле, является гармонической функцией. Во всех точках х, у, z, для которых r k, функция 1/r k удовлетворяет уравнению Лапласа (1.5).

Следовательно, потенциал Φk гравитационного поля одной материальной точки удовлетворяет уравнению (1.6).

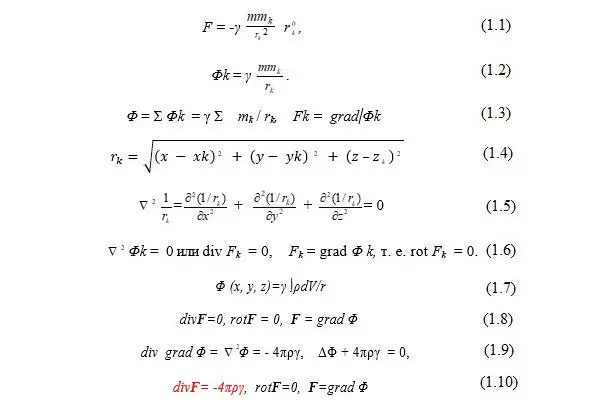
Уравнение Лапласа является линейным уравнением. Потенциал гравитационного поля Φ (х, у, z), создаваемого непрерывным распределением масс по некоторому объему V , на основании (1.3) можно написать в виде (1.7), где ρdV=dm, ρ – плотность распределения массы элемента объема dV, dm- прирост массы.

Эта функция Φ (х, у, r) удовлетворяет уравнению Лапласа Φ (х, у, r) = 0 в точках, где нет масс.

Уравнение Лапласа для Φ равносильно уравнениям (1.8).

Можно показать при весьма общих практически приемлемых допущениях относительно распределения плотности ρ , что потенциал Φ гравитационного поля (1.7) для точек х, у, z , расположенных внутри V, удовлетворяет уравнению Пуассона (1.9).

Уравнение (1.9) равносильно уравнениям (1.10).

Практически приходится обычно иметь дело со слабыми гравитационными полями, для которых уравнения поля линейны. Для таких полей в первом приближении справедлив принцип суперпозиции. Волновое уравнение слабого гравитационного поля можно получить, если добавить вторую производную по времени в уравнение (1.9), превратив уравнение Пауссона в уравнение Д"Аламбера.