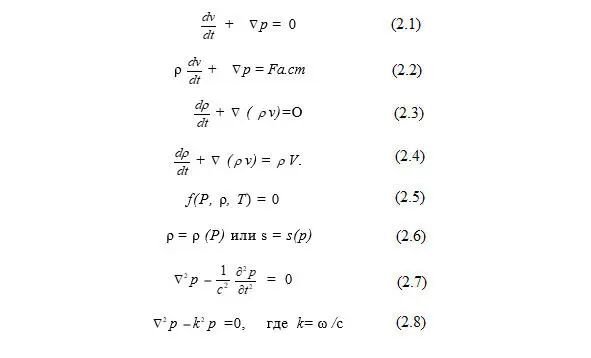Математическая модель акустического поля
Акустика – область физики, исследующая упругие колебания и волны, их взаимодействие с веществом и применение.
Во всех средах (жидких, газообразных и твердых) распространение упругих волн происходит так: частицы среды в волне приобретают скорость, деформируются, и в них возникают упругие напряжения, которые и передают волну дальше.
Акустика жидкостей и газов рассматривается на основе гидродинамики, где возмущения передаются силами давления, которые возникают при сжатии и расширении частиц. В твердых телах возникают еще и поля (сдвиговые) упругих напряжений.
Математическая модель акустического поля представлена полной системой уравнений акустики, которая состоит из уравнений движении, уравнения непрерывности и уравнения состояния. Уравнения акустики кратко можно характеризовать так. [3].
Уравнения Эйлера – уравнения движения частиц под действием сил упругости среды. Рассмотрим частицу среды малого объема, ограниченную поверхностью. Так как частица мала, а характеристики среды непрерывны, можем считать плотность по всей среде постоянной, массу частицы приравнять произведению плотности на объем. Далее, полагая, что вся частица движется как одно целое, найти ее ускорение как производную dv/dt ее скорости v по времени t. Рассмотрим давление p и сторонние cилы F а. ст,действующие на частицу со стороны окружающей среды, – силы давления.
Применяя к частице, находящейся под действием только сил давления, второй закон Ньютона и используя теорему Гаусса – Остроградского заменяя интеграл по поверхности интегралом по объему, а также учитывая непрерывности всех характеристик среды, что позволяет градиент давления на протяжении малой частицы считать постоянным, получить уравнение Эйлера (2.1).
Если помимо сил давления на среду действуют сторонние силы Fа. ст, распределенные с плотностью ρ на единицу объема, то уравнение (2.1) примет вид (2.2).
Уравнение движения среды есть нелинейное векторное уравнение первого порядка относительно характеристик среды р, v, ρ.
Уравнение неразрывности среды. Если в среде не образуется разрывов (как, например, разрывы при кавитации), то уравнение неразрывности применимо к исследуемой среде.
Рассмотрим объем среды, ограниченный неподвижной поверхностью S. Если разрывов нет, то приращение массы в объеме равно массе среды, втекшей через поверхность S. Запишем скорость приращения массы в малом объеме, массу, втекающая за единицу времени через элемент поверхности dS, равную v dS.
Заменяя интеграл по поверхности интегралом по объему, получим уравнение неразрывности в виде (2.3).
Уравнение неразрывности скалярно и, как уравнение Эйлера, нелинейно относительно характеристик среды. В дальнейшем встретятся случаи движения среды, удовлетворяющие вместо уравнения неразрывности уравнению вида (2.4).
Это уравнение можно также интерпретировать как уравнение неразрывности, но примененное к среде, куда поступает «из ниоткуда» дополнительное «стороннее» количество среды. Величину Vст называют плотностью сторонней объемной скорости: она дает дополнительный объем, поступающий за единицу времени в единичный объем.
Уравнение состояния связывает давление, плотность (или сжатие) и температуру среды. Уравнение состояния не имеет какого-либо стандартного вида для всех веществ, наподобие уравнения Эйлера или уравнения неразрывности. В общем виде уравнение можно записать в виде (2.5).
Уравнение состояния также нелинейно.
Если при данном движении среды плотность однозначно связана с давлением (так бывает обычно в акустике), то уравнение состояния можно записать в виде (2.6).
Система уравнений (2.1), (2.3) и (2.5) или (2.6) является полной системой уравнений гидродинамики.
Волновое уравнение. Полная система уравнений гидродинамики это – нелинейные, точные уравнения. В дальнейшем будем пользоваться приближенными уравнениями линейного типа. Исключая все величины, характеризующую волну, кроме давления приведем полную систему уравнений акустики к одному уравнению относительно давления p (2.7).
Это волновое уравнение второго порядка для давления, где с – скорость звука.
Если записать выражение для давления гармонического колебания волн и затем подставить его в волновое уравнение (2.7), то получим волновое уравнения Гельмгольца (2.8).
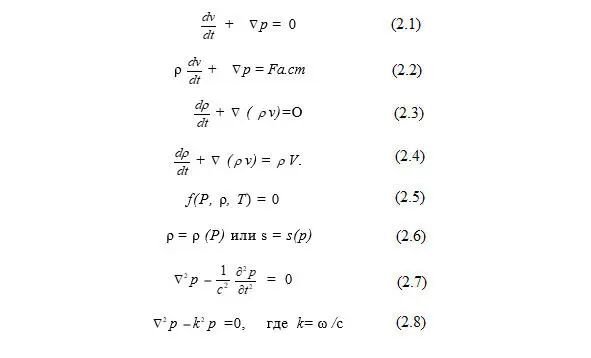
Математическая модель электромагнитного поля
Читать дальше