Сен Гук Ким - Элементы

Здесь также 120 чисел. Но 8-ми разрядный «октавный Закон» Ньюлендса был математическим законом Периодической Таблицы химических элементов до 1989 года. Поэтому и мы будем ожидать высокой периодичности во множестве химических элементов в таблице 8 × 15. На рисунке ниже представлена таблица 8 × 15 химических элементов.

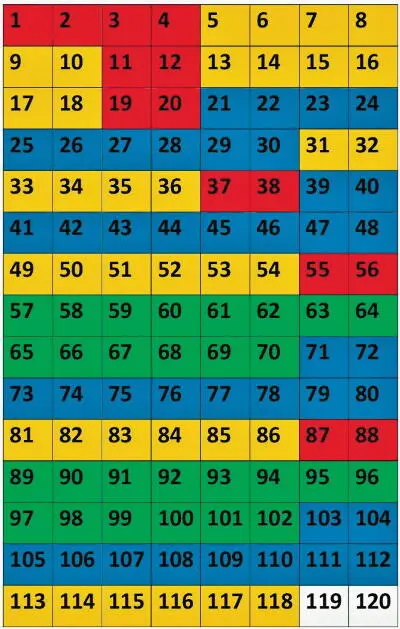
Рис. 7. Таблица 8 × 15 химических элементов

Повторяющихся строк 9 из 15 или 72 химических элемента из 118. Это составляет 61 %. Действительно большой процент периодизуемости. Но до 100 % далеко.

Если первые 1–4 химических элемента вынести за пределы таблицы, то получим:

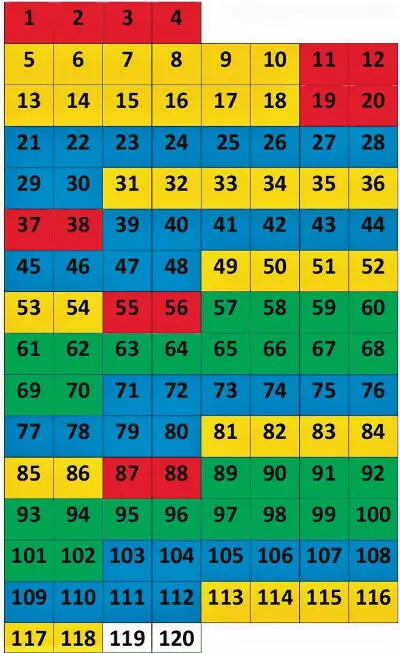
Рис. 8. Таблица 8 × 15 с вынесенными за пределы таблицы первыми 1–4 химическими элементами

Здесь мы имеем 11 периодизирующихся рядов, т. е. 88 из 118 химических элементов. Это составляет около 74,6 %, что выше предыдущего случая на 13,6 %. Хорошая периодизируемость, но также далека от 100 процентной.

16-разрядную таблицу рассматриваем в связи с тем, что она кратна 8-ми разрядной таблице, а на 8-ми разрядной таблице достигли максимальной периодичности в 74,6 %. В этом случае в таблице 128 числовых элементов. Таблица химических элементов для этого случая:

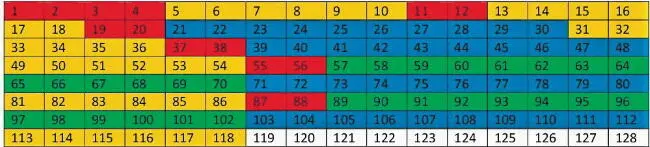
Рис. 9. Таблица 16 × 8 химических элементов

Элементы 121–128 относятся к следующему за f-бло-ком g-блоку ожидаемых химических элементов. Но их пока нет. Поэтому химических элементов и в этом случае только 118. В такой таблице имеются 4 периодизи-рующихся рядов, и в них 64 химических элемента. Они составляют примерно 54,23 %. Это намного меньше максимального 74,6 %. Уменьшать или повышать далее разрядность таблиц смысла не имеет. Мы получили весь диапазон «хорошей» периодизируемости химических элементов. К искомому результату – 100 %-му охвату всех химических элементов не подошли и близко.

Вывод:разрядность чисел не может служить основой систематизации химических элементов. Следует искать другие закономерности.

1. Квадрат натуральных чётных чисел (2n) 2при n = 1; 2; 3; 4:

(2n) 2= 4; 16; 36; 64 (1)

2. Квадрат любого числа n равен сумме последовательных нечётных чисел:

n 2= Σ(2n –1) (2)

Это подтверждается последовательной подстановкой каждого из n = 1; 2; 3; 4:

Σ(2n –1) = 1; 1 + 3; 1 + 3 + 5; 1 + 3 + 5; 1 + 3 + 5 + 7

Тогда: (2n) 2= 2[2(1); 2(1 + 3); 2(1 + 3 + 5); 2(1 + 3 + 5 + 7)], (3)

и

(2n) 2= 2(2n 2) = 2(2; 8; 18; 32) (4)

Получились числовые сдвоенности – Диады из числовых Монад: 2; 8; 18; 32.

Просуммируем все Диады (4) с учётом (2), (3) и правила: «от перестановки мест слагаемых сумма не изменяется».

Σ2(2n 2) = 2Σ2Σ(2n –1) = 2{2[(1) + (1 + 3) + (1 + 3 + 5) + (1 + 3 + 5 + 7)]} = 2(2) + 2(2 + 6) + 2(2 + 6 + 10) + 2(2 + 6 + 10 + 14) = 2(2) + 2(6 + 2) + 2(10 + 6 + 2) + 2(14 + 10 + 6 + 2)

Полученный результат представляет полное количество KD чисел в четырёх Диадах из пар (2 перед скобками) Монад, которые состоят последовательно из 1, 2, 3, 4 слагаемых (в скобках). В сумме они составляют:

K D= 2(2) + 2(6 + 2) + 2(10 + 6 + 2) + 2(14 + 10 + 6 + 2) = 120 (5)

С учётом (3) формулу (4) можно записать как последовательность количества K Nномеров N в Монадах последовательности n = 1; 2; 3; 4 Диад:

K N= 2(2n 2) = 2Σ2(2n –1) = 2[2(1), 2(3 + 1), 2(5 + 3 + 1), 2(7 + 5 + 3 + 1)] (6)

Произведя суммирование и раскрытие скобок в правой части формулы (6), получим распределение количества K Nномеров N в n = 1; 2; 3; 4 Диадах:

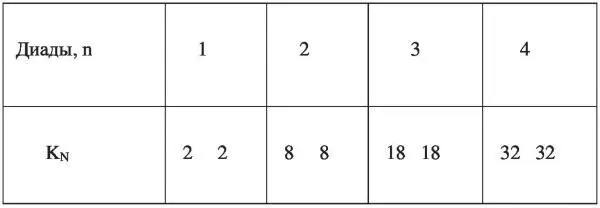
Это именно количества номеров, которые не обязательно должны следовать по определённому нарастающему порядку в монадах. Номера же должны последовательно нарастать. Номера N, в отличие от K Nпо формуле (6), должны выстраиваться в последовательных монадах 1–4 Диад по этой же простой формуле:

N = 2Σ2(2n –1), (7)

но в последовательно нарастающем порядке от 1 до 120.

Все значения K Nчётные. Поэтому можно построить геометрическое воплощение формул (5) и (6) в виде вертикально-симметричной последовательности 20-ти рядов ячеек-квадратиков 8-ми Монад для 1-120 номеров N в n = 1; 2; 3; 4 Диадах-Уровнях сверху вниз:

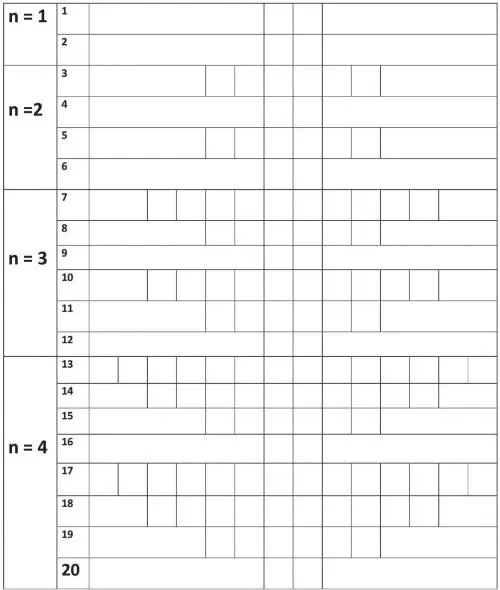
Рис. 10. Вертикально-симметричное 4-Уровневое распределение ячеек-квадратиков для 1-120 номеров в 20-ти рядах 8-ми Монад по формуле (6)