Геннадий Степанов - Искусственный разум. Параллельная специализированная гибридная машина. Метод точного мгновенного решения NP задачи

Таблица 3. Определение весов грузов

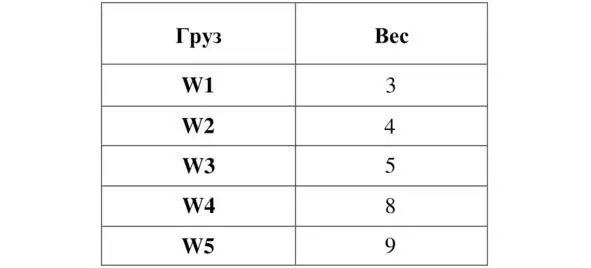
Для данного множества грузов максимальная мощность подмножеств грузов М = 3.

Согласно моего метода, для получения оптимального решения задачи о ранце, необходимо чтобы:

m = ( М+ 1) /2 для M для нечётных;

m = M /2+1 для M для чётных.

Для данного примера задачи о ранце: М = 3, m = 2.

Значения цены грузов P зададим в виде таблицы 4.

Таблица 4. Определение цены грузов

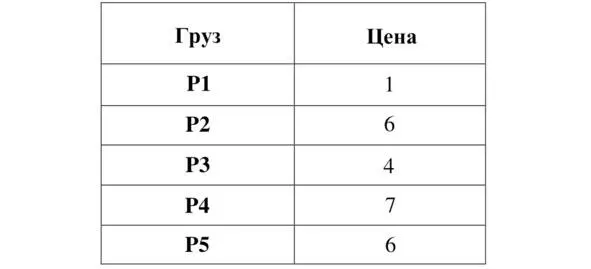
С помощью метода неявного перебора был получен оптимальный результат для данного примера задачи о ранце:

W = W2 + W4 = 4 + 8 = 12

P = P2 + P4 = 6 + 7 = 13

Занесём определённый упорядоченный вектор грузов относительно значений весов грузов и их цены в таблицу 5.

Произведём объединение грузов из множества грузов в подмножества грузов по два и по три.

Полученные упорядоченные вектора подмножества грузов по два и по три и их значений суммарных весов грузов и цен занесём в таблицу 5.

Таблица 5. Определённый и полученные упорядоченные вектора грузов

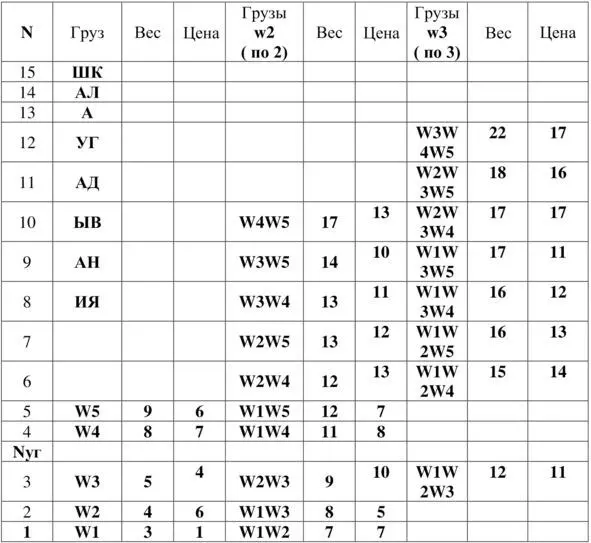
Из таблицы 5 видно, что для определения глобального оптимального результата в данном примере задачи о ранце: для данного метода достаточно чтобы N уг= 3.Искомый результат:

W = W1 + W2 + W3 = 3 + 4 + 5 = 12

P = P1 + P2 + P3 = 1 + 6 + 4 = 11

Таким образом, без перебора вариантов решения задачи о ранце, находим данным методом глобальный оптимальный результат данного примера задачи о ранце.

Основываясь на данных из таблицы, определим зависимость числа подмножеств по три (Kw3) с суммарным весом грузов больше или равно W = 12, от числа угадывания (N) на шкале угадывания (Nm) для данного метода.

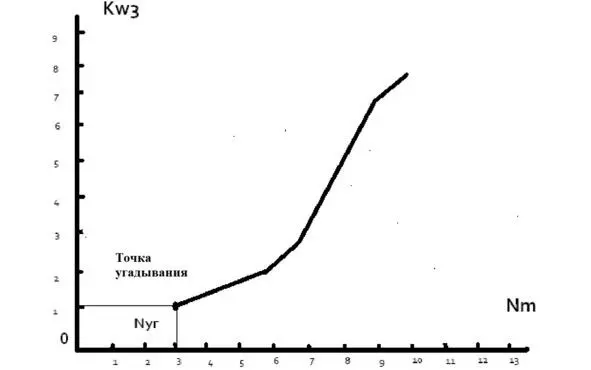
Рис. 4.13. Выявленная зависимость между К w3 и N m.

Где К w3 – количество подмножеств грузов по три, с суммарным весом грузов больше или равно W.

N m – шкала угадывания количества подмножеств грузов.

N уг – количество угаданных подмножеств грузов.

Согласно данного метода определим локальное оптимальное решения задачи о ранце для значений:

М = 2 и N уг = 4.

Рассмотрим таблицу 6 для значений М = 2 и N уг = 4.

Таблица 6. Определённый и полученный упорядоченный вектор грузов для М = 2 и N уг= 4.

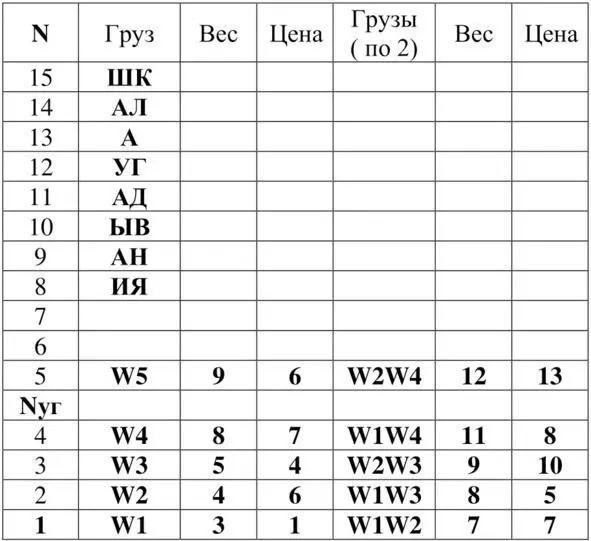
Из таблицы 6 определим локальное оптимальное решения задачи о ранце:

W = W2 + W4 = 4 + 8 = 12

P = P2 + P4 = 6 + 7 = 13

Согласно метода, определим локальное оптимальное решения задачи о ранце для значений М = 1 и N уг= 5 согласно таблицы 7.

Таблица 7. Определённый вектор грузов для

М = 1 и N уг = 5

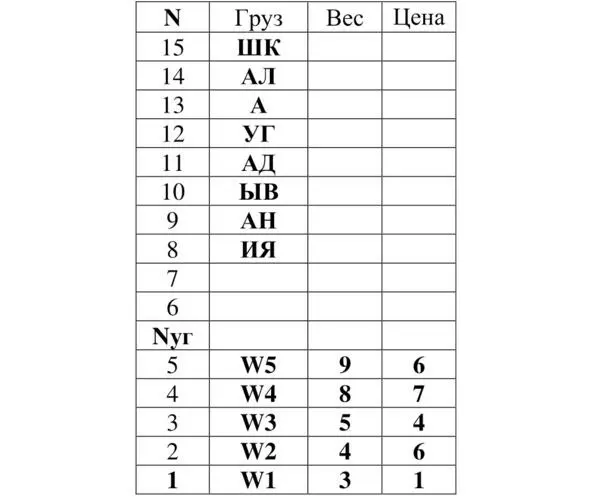
Из таблицы 7 определим локальное оптимальное решения задачи о ранце для М = 1 и N уг = 5 :

W = W4 = 8

P = P4 = 7

Исходя из вышеизложенного выбираем локальный оптимальный результат данного примера задачи о ранце:

W = W2 + W4 = 4 +8 = 12

P = P2 + P4 = 6 + 7 = 13.

Таким образом, без перебора вариантов решения задачи о ранце, находим данным методом локальный оптимальный результат и глобальный оптимального результат для данного примера задачи о ранце с помощью моего метода. Определение лучшего результата требует выполнение дополнительных условий. Необходимо определить, что для нас является более важным, число грузов или их ценность.

Что и требовалось доказать.

Задача о назначениях – одна из фундаментальных задач комбинаторной оптимизации. Задача состоит в поиске минимальной суммы дуг во взвешенном двудольном графе.

В наиболее общей форме задача формулируется следующим образом:

Имеется некоторое число работ и некоторое число исполнителей. Любой исполнитель может быть назначен на выполнение любой одной работы, но с неодинаковыми затратами. Нужно распределить работы так чтобы выполнить работы с минимальными затратами.