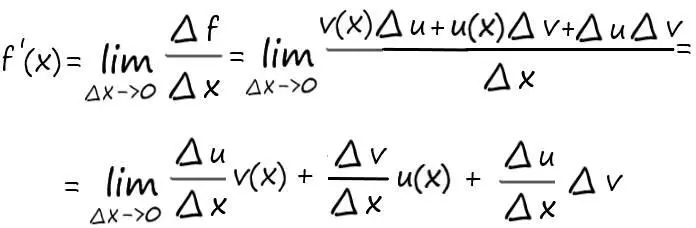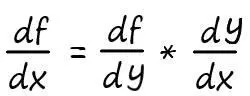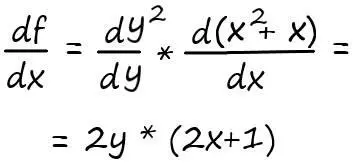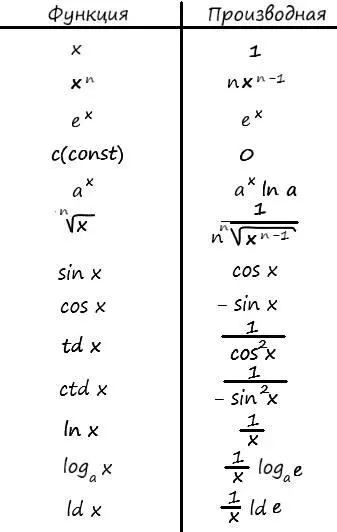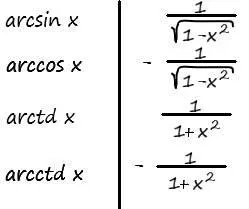Далее имеем:
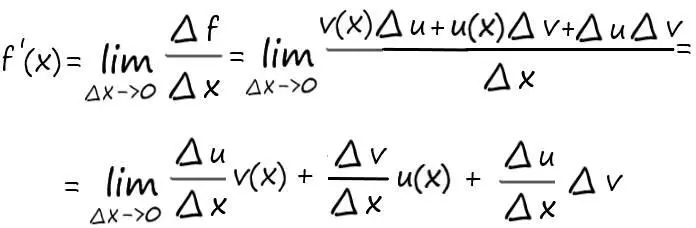
Первое слагаемое стремиться к u′(x) v(x). Второе слагаемое стремиться к v′(x)* u(x). А третье, в дроби ∆ u /∆ x, в пределе даст число u′(x), а поскольку множитель ∆vстремиться к нулю, то и вся эта дробь обратится в ноль. А следовательно, в результате получаем:
f ′( x ) = u ′ ( x ) v ( x ) + v ′ ( x ) u ( x )
Из этого правила, легко убедиться, что:
( c * u )′ = c ′ u + c u ′ = c u ′
Поскольку, с– константа, поэтому ее производная равна нулю (c′ = 0).
Зная это правило мы без труда, найдем изменение скорости второго примера.
Применим к выражению правило дифференцирование суммы:
s ′ ( t ) = (0,2t) ′ + (1,5) ′
Теперь по порядку, возьмём выражение – (0,2t) ′. Как брать производную произведения константы и переменной мы знаем:
(0,2t) ′ = 0,2
А производная самой константы равна нулю – (1,5) ′ = 0.
Следовательно, скорость изменения скорости, второго примера:
s ′ ( t ) = 0,2
Что совпадает с нашим ответом, полученном ранее во втором примере.
Дифференцирование сложной функции
Допустим, что в некоторой функции, yсама является функцией:
f = y²
y = x²+x
Представим дифференцирование этой функции в виде:
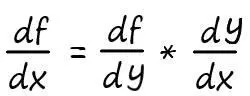
Нахождение производной в этом случае, осуществляется в два этапа.
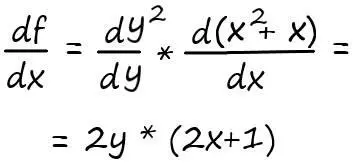
Мы знаем, как решить производную типа: dy²/dy = 2y
А также знаем, как решать производную суммы: х² + х = (х²)′ + х′ = 2х+1
Тогда:
2(x²+x) * (2х+1) = (2х²+2х) * (2х+1) = 4х³+6х²+2х
Я надеюсь, вам удалось понять, в чем состоит суть дифференциального исчисления.
Используя описанные, методы дифференцирования выражений, вы сможете понять механизм работы метода градиентного спуска.
В качестве небольшого дополнения, приведу список наиболее распространённых табличных производных:
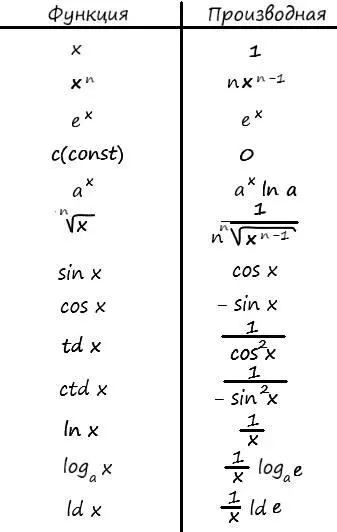
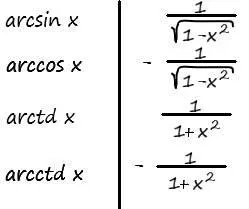

Зачем нам дифференцировать функции
Еще раз вспомним как мы спускаемся по склону. Что в кромешной тьме, мы хотим попасть к его подножью, имея в своем арсенале слабенький фонарик.
Опишем эту ситуацию, по аналогии с математическим языком. Для этого проиллюстрируем график метода градиентного спуска, но на этот раз применительно к более сложной функции, зависящей от двух параметров. График такой функции можно представить в трех измерениях, где высота представляет значение функции:
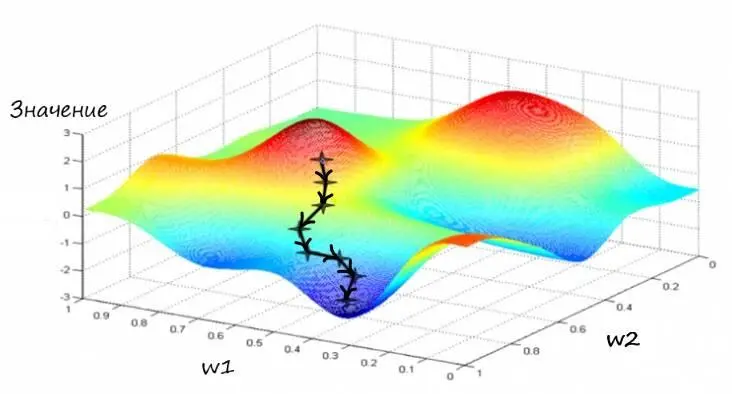
К слову, отобразить визуально такую функцию, с более чем двумя параметрами, как видите, будет довольно проблематично, но идея нахождения минимума методом градиентного спуска останется ровно такой же.
Этот слайд отлично показывает всю суть метода градиентного спуска. Очень хорошо видно, как функция ошибки объединяет весовые коэффициенты, как она заставляет работать их согласованно. Двигаясь в сторону минимума функции ошибки, мы можем видеть координаты весов, которые необходимо изменять в соответствии с координатами точки – которая движется вниз.
Представим ось значение, как ось ошибка. Очень хорошо видно, что функция ошибки общая для всех значений весов. Соответственно – координаты точки значения ошибки, при определенных значениях весовых коэффициентов, тоже общие.
Читать дальше