Множество – одно из основных, фундаментальных понятий математики, которое нельзя определить через другие понятия, поэтому его можно только более или менее доходчиво описать. Множество – это любое собрание определенных и различимых между собой объектов мыслимое как единое целое. Эти объекты называются элементами или членами множества. Существенно для понимания, что здесь собрание предметов само рассматривается как один объект. Множество деревьев – это сад или лес, множество учащихся – класс или школа, множество работников предприятия – коллектив, множество птиц – стая. Для обозначения множеств обычно используют большие латинские буквы. Множество может быть конечным, когда конечно число входящих в него элементов. Например, множество букв русского алфавита конечно и состоит из 33 элементов. С другой стороны, множество всевозможных упорядоченных наборов букв бесконечно, если не накладывать ограничений на длину этих наборов.
Конечное множество можно задать простым перечислением его элементов. Для этого принята следующая форма записи: R ={а, б, в, г, д, е, ё, ж, з, и, й, к, л, м, н, о, п, р, с, т, у, ф, х, ц, ч, ш, щ, ъ, ы, ь, э, ю, я}.
Так мы задали множество букв русского алфавита. Определим подобным образом еще несколько конечных множеств, состоящих из тех же букв и собранных по некоторым индивидуальным для каждого множества признакам:
G ={а, е, ё, и, о, у, ы, э, ю, я},
S ={б, в, г, д, ж, з, к, л, м, н, п, р, с, т, ф, х, ц, ч, ш, щ},
P ={й},
Z ={ъ, ь},
D ={б, в, г, д, ж, з, л, м, н, р},
T ={к, п, с, т, ф, х, ц, ч, ш, щ},
X ={ж, ш, ч, щ}.
Другой способ задания множества – описательный. Нужно сформулировать предложение, которое описывает данное множество так, что его нельзя спутать ни с каким другим и о любом объекте можно точно сказать принадлежит ли он этому множеству или нет. Тогда перечисленные выше множества букв будут определяться так:
G – множество гласных букв русского алфавита,
S – множество согласных букв,
P – множество полугласных букв,
Z – множество букв, которым не соответствует никакого звука в устной речи, иначе говоря – множество знаков,
D – множество звонких согласных,
T – множество глухих согласных,
X – множество шипящих согласных.
Бесконечное множество нельзя задать перечислением всех его элементов, но часто можно описать их свойства. Встречаются и конечные множества с той же степенью неопределенности. Например, до сих пор ученым не удалось расшифровать письменность острова Пасхи. До нас дошли несколько десятков табличек, покрытых рисуночными значками, вырезанными зубом акулы по дереву. Эти письмена аборигены называют кохау ронго-ронго – «говорящее дерево». Множество знаков-иероглифов в письменности острова Пасхи, можно определить этим предложением, но нельзя с уверенностью и точно перечислить, хотя это множество заведомо конечное.
Множества G , S , …, X содержат разное количество элементов и среди них есть одно, для которого используется специальное название. Множество, содержащее единственный элемент называется одноэлементным или единичным множеством . Речь идет о множестве P ={й}, которое содержит единственную букву, обозначающую полугласный звук, то есть звук не образующий слога. Можно задать и пустое множество , в котором не содержится ни одного элемента. Так как это множество никак не характеризуется своими отсутствующими элементами, то логично утверждать, что может быть только одно множество, не имеющее элементов. Для его обозначения принят специальный знак Ø.
Отношения между объектами и множествами описываются понятием принадлежности. Для записи этого отношения есть два специальных знака принадлежит и не принадлежит .
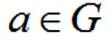
означает, что буква а – гласная и является элементом множества гласных букв, то есть принадлежит ему.
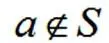
означает, что буква а не является согласной и не принадлежит множеству согласных букв. В качестве сокращения можно записывать отношение принадлежности сразу для нескольких элементов:
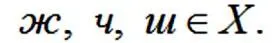
Отношения между множествами определяются следующими утверждениями.
Два множества равны в том и только в том случае, когда они состоят из одних и тех же элементов. Для обозначения равенства двух множеств применяется обычный знак равно {a, e, o}={e, o, a}. Порядок расположения элементов при их перечислении не важен, он не меняет состава множества.
Читать дальше
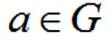
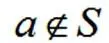
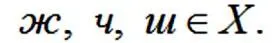

![Владимир Трошин - Княжич [СИ]](/books/404433/vladimir-troshin-knyazhich-si-thumb.webp)









