Сергей Бердышев - Открытия и изобретения, о которых должен знать современный человек

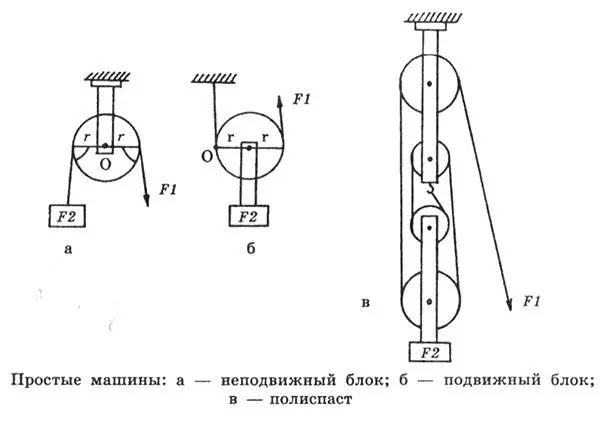
Важнейшим свойством этих простых механизмов является их способность восстанавливать и поддерживать равновесие тел за счет приложенных сил. Поскольку равновесие означает баланс сил, то назначение простых машин заключается в изменении направления или величины затрачиваемых сил при сохранении постоянной работы.

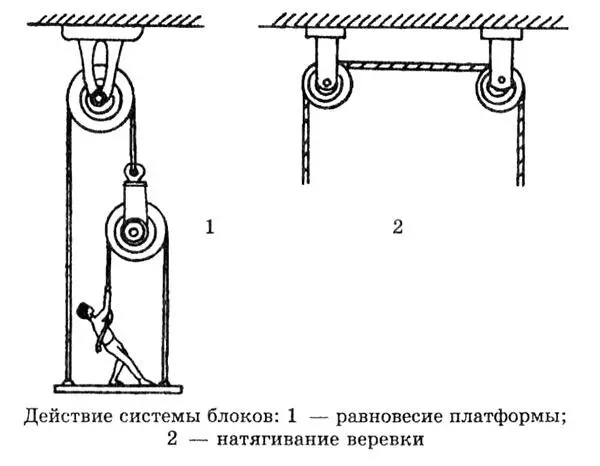
Чтобы познакомиться с возможностями простых машин, рассмотрим две нехитрые системы неподвижных блоков. Представим себе, что человек пытается с помощью системы из двух блоков — неподвижного и подвесного — поддержать себя и подвесную платформу, т. е. уравновесить собственный вес и вес платформы посредством мускульной силы. При этом подвесной блок, на который воздействует мускулатурой человек, связан с канатом, перекинутым через неподвижный блок. Возможно ли это?

В принципе такое явление вполне допустимо. В системе взаимодействуют несколько сил — вес человека, вес платформы, а также силы натяжения отрезков каната. Представим, что система уже находится в равновесии, и выясним условия такого состояния. Отрезки каната, перекинутого через подвесной блок, натянуты с одинаковой силой, поскольку являются продолжением одного каната. То же самое можно сказать и про концы каната, перекинутого через неподвижный блок.

С каждого блока спускается по отрезку от каждого из канатов, подсоединенному к платформе. На эти два отрезка действуют ее вес и вес человека, которые мы буквенно обозначим P и P’ . Так как в системе установлен баланс сил, то сумма весов P и P’ уравновешена силами натяжения. Примем за F силу натяжения, приходящуюся на скрепленный с платформой отрезок, относящийся к подвесному блоку. Тогда эта сила равняется мускульной силе человека. А сила натяжения в закрепленном отрезке неподвижного блока будет численно равна сумме двух этих сил, т. е. 2F . Таким образом, результирующая сила натяжения равна 3F .

Сила человека была утроена системой блоков! Если система пребывает в равновесии, то суммы противонаправленных сил количественно равны. Сложив вес человека и платформы, мы получим величину, равную учетверенной силе человека. Запишем это в виде уравнения:

P + P’ = 3F ,

где P’ — вес человека, а P — вес человека, а P — вес платформы. Физически крепкий мужчина способен удержать вес, равный собственному:

F = P .

Если справедливо предположить, что все усилия нашего воображаемого человека на платформе идут на удержание собственного веса, то получается, что ее вес равняется удвоенной силе человека:

P = 2F.

Итак, чтобы человек удержал платформу в равновесии посредством описанной системы блоков, вес платформы не должен превышать мускульную силу человека более чем в 2 раза. Если же вес платформы много меньше мускульной силы человека или, по крайней мере, равен ей, значит, человек может применить неполную силу для поддержания равновесия. Как видно, блок не так уж прост.

Обращает на себя внимание вертикальное натяжение канатов, которое максимально. Натянуть же с помощью двух неподвижных блоков веревку в горизонтальном положении столь успешно нельзя, т. к. она все равно будет немного провисать. А причиной тому является баланс сил в системе блоков. Провисание вызывает сила тяжести, направленная вертикально. Поэтому никакая приложенная к горизонтали сила на веревку не подействует и силу тяжести не скомпенсирует.

Как видно, описанные выше системы меняют направление сил или меняют их величины. Принципы действия простых машин легко объяснить на наиболее типичных устройствах — неподвижном и подвижном блоках. У неподвижного блока силы приложены к двум точкам, которые лежат на равных расстояниях от центра, служащего точкой опоры. Данные силы всегда количественно равны друг другу, т. к. взаимно уравновешиваются. Однако направление их действия неодинаково. То есть неподвижный блок меняет направление силы, в этом заключается выигрыш.

Теперь рассмотрим подвижный блок. У него точка опоры лежит на краю колеса, на середину его приходится нагрузка, а на другой край — противодействующая сила. Все три точки — опоры и приложения сил — лежат на одной прямой, совпадающей с диаметральной хордой окружности колеса блока. Нетрудно убедиться, что неподвижный блок меняет величину приложенной силы. Расстояние от точки опоры до точки приложения сил неодинаково, и мускульная сила приложена к точке, что находится на расстоянии 2r.