Сергей Бердышев - Открытия и изобретения, о которых должен знать современный человек

Затем машины, действие которых основано на принципе рычага, стали использоваться в строительстве повсеместно. Естественно, особое значение они получили в Древней Элладе, т. к. греки уважали архитектуру. Эта наука в их представлении была связана с одной из «идеальных» наук — геометрией. Конструирование механических устройств не было, однако, столь почетным делом. По этой причине рычагом пользовались, не пытаясь объяснить его свойств.

Некоторые древнегреческие мыслители предпринимали попытки разгадать тайны рычага, но все эти начинания оказались тщетны по той причине, что древние подходили к проблеме с предвзятым суждением о свойствах этого простого устройства. Вскоре рычаг был объявлен магическим инструментом, потому что его работа основывалась на полумистических свойствах круга. Дело в том, что концы плеч рычага описывают в пространстве во время своего движения дуги окружностей. А круг и окружность почитались в Древнем мире как священные и волшебные фигуры, ведь по кругу двигались небесные светила.

Круг был «идеален» во всех отношениях, а потому ссылкой на него легко можно было объяснить все самое непонятное в природе и жизни людей. Закон рычага предстояло открыть великому древнегреческому геометру III в. до н. э. Архимеду, жившему в городе Сиракузы на Сицилии. Архимед первым приподнял завесу тайны над магическим кругом, обнаружив число «пи», и поэтому относился к геометрии без излишней предвзятости и идеализации.

Кроме того, Архимед обладал чрезвычайно широким кругозором и занимался практически всеми вопросами существовавших в ту эпоху направлений геометрической науки. Архимед работал над правилами построения фигур, развивал теорию геометрии, конструировал осадные и строительные машины, изучал центры равновесия (центры тяжести), рассчитывал планетарии, т. е. глобусы звездного неба. Единственной отраслью современной ему геометрии и механики, в которой ученый себя никак не проявил, было изобретение механических игрушек.

Таковы предпосылки, благодаря которым Архимед первым описал сущность работы рычажного устройства и на этом основании сформулировал закон рычага. Рычагом называется любой жесткий стержень для приподнимания и перемещения тяжестей. Он имеет точку опоры или ось скольжения, позволяющую ему осуществлять передвижку предметов. Участки стержня, к которым приложены противодействующие силы, называются плечами рычага. Длина каждого плеча равна протяженности отрезка стержня между точкой опоры и точкой приложения силы.

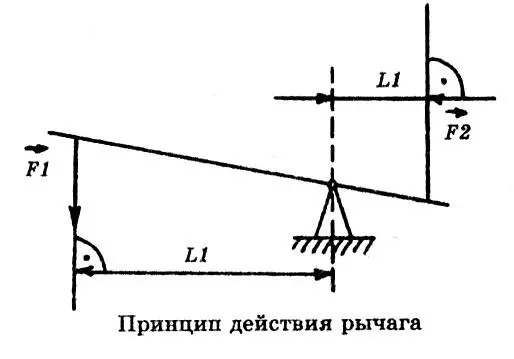
Одной из сил является вес тяжелого тела, которое необходимо переместить. Вторая сила, приложенная к другому плечу, — мускульная. Эту силу развивает человек, работающий с рычагом. Естественно, такая схема сильно упрощена, поскольку рычаги бывают самыми разными, и силы на них действуют также различные. Работа равняется, как и в предыдущих случаях, произведению расстояния на силу. Тело смещается благодаря рычагу в вертикальном направлении.

Однако это расстояние, как несложно убедиться, зависит от длины плеча рычага. Это следует из равенства треугольников, а треугольниками в данном случае являются воображаемые фигуры, отражающие перемещение точек приложения сил и точки опоры. Следовательно, чем ближе к точке опоры вес тяжелого тела и чем дальше приложение мускульной силы, тем больший выигрыш получает человек. Впрочем, понятие выигрыша относительно, т. к. выигрыша в работе рычаг не дает. В этом он схож с любым простым механизмом.

В рассмотренном случае, когда к длинному плечу приложена мускульная сила, происходит выигрыш в силе: малой силой можно уравновесить большую. Но есть рычаг другого рода, который дает выигрыш в расстоянии. В этом случае мускульная сила приложена к короткому плечу. Перемещать слишком тяжелые предметы нельзя, зато свободно передвигаемые таким рычагом тела могут смещаться на большие расстояния. «Золотое правило» механики действует и здесь. Если есть выигрыш в силе, то будет проигрыш в расстоянии, и наоборот.

Многие люди ошибочно полагают, что тела одинакового веса всегда уравновешиваются рычагом. Отнюдь, равновесие между одинаковыми телами наступает лишь в одном случае — когда плечи рычага равны по длине. В остальных случаях равенства не наступает. Это неудивительно. Соотношение сил равняется соотношению длины плеч рычага. То есть при равных силах, когда соотношение равно 1, для установления баланса необходимо, чтобы соотношение длин плеч количественно равнялось той же величине. Единицу в пропорции можно получить при единственном условии: когда длины плеч одинаковы.