Константин Крамаренко - Вещи не то, чем кажутся. 100 фреймов УНИВЕРСУМА

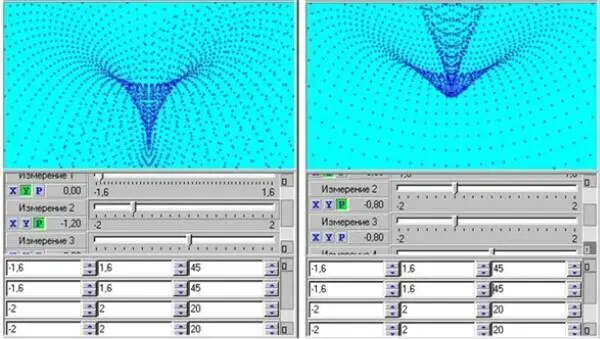
Двухмерные образы катастроф. Эллиптическая и параболическая омбилики

При стратификации успеваемости существуют довольно устойчивые группы, соответствующие как максимуму (отличники и близкие к ним студенты), так и слой студентов, соответствующий минимуму – имеющих неудовлетворительную успеваемость и занимающихся по нижней грани оценки удовлетворительно. Они находятся на разных листках топологической поверхности достижений. С точки зрения теории катастроф, в педагогическом процессе основные усилия по контролю знаний и обучению должны быть сконцентрированы на тех студентах, которые находятся в бифуркационной зоне. Так как студенты, имеющие посредственную успеваемость, могут скачком перейти в область хороших и отличных достижений, а хорошо успевающие студенты очень быстро выйти из опасной зоны бифуркации и обрести устойчивый ранг высоких оценок. Располагая данными IQ студентов, параметрами, обеспечивающими качество учебного процесса и используя методы теории катастроф, можно будет прогнозировать, и в определённых пределах более эффективно управлять качеством образования.

Практическое применение теории катастроф заключается в том, что огромное количество явлений, встречающихся в мире, она позволяет свести к очень ограниченному набору стандартных форм, и уже с их помощью провести количественные и качественные оценки динамично изменяющихся феноменов. Так как методы теории катастроф универсальны, они могут использоваться в сфере политики, экономики, управления, медицины, образования и т. п. Таким образом, научное познание получает новые эффективные инструменты для исследования феноменов реальности, до настоящего времени недоступных традиционным методикам и технологиям.

Статус математики в отношении природных процессов долгое время был не определён. В действительности нет точек, прямых линий, идеальных кругов и других фигур геометрии Евклида. С точки зрения здравого смысла, математика – это игра разума и задача познания с целью лишь описания явлений и их классификации. Поэтому древнегреческое знание не развило физику и естествознание. Создать физику и другие естественные науки – значит применить к действительности однородные точные математические и геометрические законы.

Только в Новое время Галилей, Ньютон и их последователи смогли обнаружить эти формы в механическом движении и простых механических системах. Тем не менее многие природные системы обладают огромной степенью сложности, несравнимой с использованием простых образов классической геометрии, поэтому их моделирование на такой основе оказывается невозможным. Действительно, как построить модели кроны деревьев, горного хребта, изрезанной береговой линии в объектах евклидовой геометрии? Как смоделировать сложные биологические объекты, обладающие многообразной конфигурацией, такие как нейронная сеть, система кровообращения, ацинусное строение легких, структура почек?

Столь сложной оказывается и динамическое поведение природных процессов, например, турбулентность, ритмы сердца и головного мозга. Для моделирования подобных явлений в конце XX века был создан новый тип геометрии, получившей название фрактальной. Термин фрактал был введён американским математиком Бенуа Мандельбротом в 1983 году, когда вышла его книга «Фрактальная геометрия природы». Фракталы – это, прежде всего, язык геометрии, но они выражаются в алгоритмах, наборах своего рода математических процедур, которые трансформируются в геометрические формы с помощью компьютеров. Основной принцип строения фрактала «всё во всём» или, как отмечают математики, он обладает инвариантной структурой относительно масштабирования. Это значит, что фрактал проявляет одинаковое строение на разных уровнях масштаба и, кроме этого, обладает дробной размерностью, в отличие от линий и площадей, имеющих целостное значение.

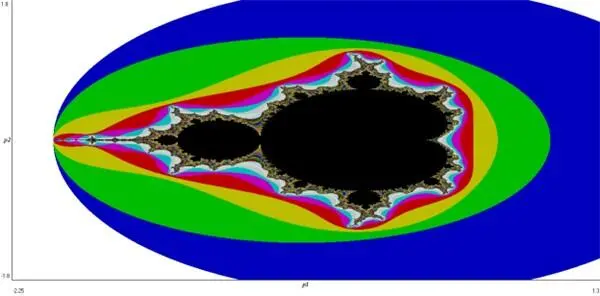
Множество Мандельброта. Построено в программе WinSet 3.0

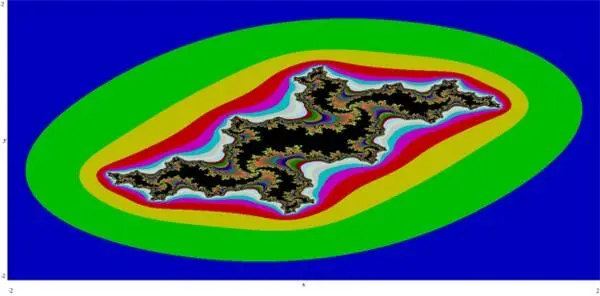
Множество Жюлиа. Построено в программе WinSet 3.0