Игорь Брыгов - Шахматы. Первое приближение

Другая разновидность проходной пешки – это защищенная проходная пешка, называется так, поскольку защищается своей соседкой-пешкой, при этом её потенциальные сторожа для «теплой встречи», место встречи уже пробежали. Пример. Белые – пешки a4, b5, c4– черные пешки a5, c5, пешка b5– защищенная проходная пешка. Количество баллов для такой пешки = 8 (восемь) активностей обычной пешки. Правда, будет и для такой пешки ряд исключений (если она надежно блокирована королем соперника от 8 стоимостных пешек остается пшик. Защищенная проходная пешка бывает как открытой (видимой), так и закрытой (без первоначального явного признака). Такая пешка образуется в динамике движения, или ее можно придумать (если хватит фантазии).

Существует также сдвоенная (строенная) по вертикали пешка – ее стоимость падает по сравнению с обычной пешкой (0,5) обычной пешки. Балансы мы будем считать в следующей главе.

3) Сколько у тебя есть времени? Понятно, если у тебя есть здоровье, деньги, но нет времени – твоей победы не состоится. Подробнее об этом через одну главу.

1) Назовите участников пешечных окончания.

2) Какое количество участников пешечного окончания может быть? От(минимум) и до(максимум)?

3) Перед вами стоит выбор из двух переменных: здоровый король и больная пешка или больной король и здоровая пешка? Ваши действия.

Попробуйте придумать другой выбор (размер вашей фантазии – может восхитить всех учеников в классе!).

4) Вы потеряли здоровье, можно ли купить себе: еще кусочек жизни?

а) Еще одну жизнь, никому не принадлежащую?

б) Часть чужой жизни?

в) Чужую жизнь?

5) Как течёт (идёт) время?

а) Линейно?

б) Или как-то иначе (не по прямой линии)?

Я долго скрывался от тебя. Но «проболтался». Значит, пора знакомиться! Привет, я – Привереда!

Ты думаешь, что мы не знакомы??? Ошибаешься!

Я… Я есть в каждом человеке. И ты – не исключение!

Помнишь, когда ты сделал поделку своими руками в подарок дорогому человеку?

Все тебя хвалили. А я на ушко шептал тебе: «Неправильно они хвалят. Ведь я мог лучше сделать!». Помнишь, когда тебе предлагали одноклассники делать как все? Именно я в тебе говорил: «А зачем мне делать как все?»… Да, да, это Я любитель неудобных и честных вопросов. Это Я твоё собственное желание не соглашаться с чем-либо в принципе…

Ты думаешь, что Я плохой? Нет! Именно Я помогаю тебе стать лучше! Благодаря моим неудобным вопросам, благодаря моей неудовлетворенности тобой, рождается желание думать, учиться и становиться лучше во всех отношениях! И путь к успеху – это наш совместный путь!

Настало время поговорить и показать четкие правила в пешечных окончаниях. Первое правило квадрата гласит, что если король (диаграмма 6 к правилу квадрата) при своем ходе не попадает в квадрат проходной пешки соперника, значит, пешка превращается на поле конечного ряда в фигуру (на практике это почти всегда ферзь). В диаграмме при своем ходе король черных попадает в квадрат белой пешки – ход g3, а при ходе белых белая пешка, сделав ход b4, становится недосягаемой для черного короля.

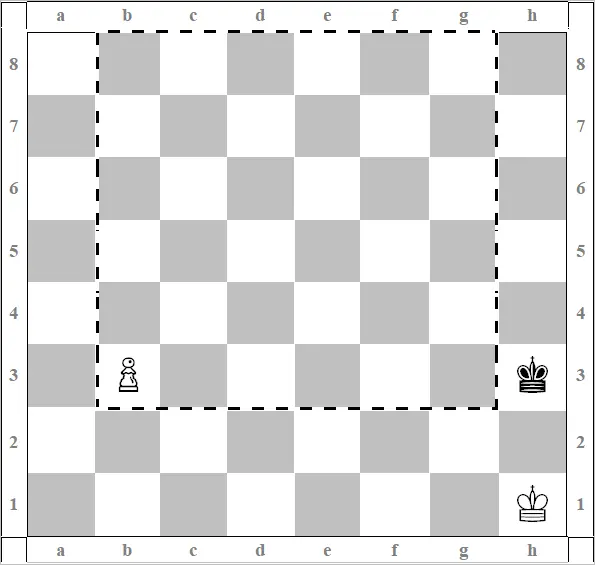
Диаграмма 6

Правило подвижного квадратакасается двух пешек, но на некотором расстоянии друг от друга (от одного до двух полей между пешками, находящимися на некотором расстоянии от пунктов превращения) – оно гласит следующее: если квадрат (со стороной проведенной через две пешки) касается крайнего ряда (поля превращения), то король противоположной стороны появлению ферзя не может помешать; если квадрат (со стороной проведенной через две пешки) не касается последнего ряда, то король может уничтожить обе пешки.

Это хорошо видно на диаграмме 7. Ход белых. Дистанция для черных пешек самая невыгодная. 1) Кра4– d4, 2) Крb3– и далее король с4, затем :d4, затем идет к пешке а5(кстати, и при ходе черных результат будет тот же (но это, читатель, попробуй самостоятельно). Поэтому они потеряются обе. Почему мы рассматриваем позиции подвижного квадрата с положительным итогом для короля так внимательно? Они, как правило, оказываются исключениями, когда в любой пешечной позиции мы будем считать пешечный баланс.