В свободно падающей системе отсчета выполняются хорошо известные законы Специальной теории относительности. Поэтому существует простой способ узнать, как то или иное явление протекает в гравитационном поле. Нужно сначала перейти мысленно от исходной к свободно падающей системе отсчета, а это можно сделать в любой точке пространства-времени, за исключением сингулярностей (о них мы расскажем позже). После перехода можно легко на основании Специальной теории относительности описать физическое явление или процесс и затем выразить его найденные характеристики через искривленные координаты исходной системы отсчета. Таким путем Специальная теория относительности связана с Общей теорией относительности. Специальная теория относительности действует локально в свободно падающих системах отсчета.
Следует отметить, что ускорение эквивалентно гравитации, как правило, лишь локально, в малых участках пространства. Нельзя, например, с помощью ускорения одного лифта скомпенсировать все гравитационное поле Земли, так как сила притяжения Земли направлена к ее центру, силы в разных точках вдоль поверхности Земли не параллельны, и поэтому ускорение в одном направлении не может скомпенсировать их все. Кроме того, существуют явления, такие как угловой момент или спин элементарной частицы, которые могут чувствовать кривизну пространства-времени даже в одной точке. Поэтому необходимо уточнить, что не всякое гравитационное поле эквивалентно ускорению.
Принцип эквивалентности сыграл важную роль при создании Общей теории относительности. Он послужил Эйнштейну прекрасной подсказкой и путеводной нитью. Но сейчас принцип эквивалентности уже не кладется в основу Общей теории относительности при ее формулировке. В более строгом подходе утверждается, что наше пространство-время описывается римановой геометрией, и в некоторых частных случаях выполняется принцип эквивалентности. Выполняется он либо точно, но только для однородного поля, либо приближенно в малом масштабе.
После того, как Эйнштейн догадался, что гравитация – это искривленное пространство-время, он несколько лет искал уравнения, которые управляют этим искривлением. И вот в конце 1915 г. уравнения гравитационного поля были, наконец, написаны. Эти уравнения показывают, какое гравитационное поле создается распределением вещества. И в этих же уравнениях заключены правила движения вещества в гравитационном поле.
Уравнения Эйнштейна обобщают закон всемирного тяготения Ньютона, который можно получить из них в случае слабых полей и медленных движений, то есть, в «ньютоновском пределе». Как мы уже знаем, строго говоря, никакой силы тяготения нет, а есть движение в искривленном пространстве-времени. Но рассуждать в терминах сил в ньютоновском пределе очень удобно и наглядно. И в ньютоновском пределе нет надобности знать Общую теорию относительности и пользоваться ее сложными уравнениями. Поэтому говорить в этом пределе о «силе притяжения» вполне законно. А вот для большинства сильных полей тяготения, когда велико искривление пространства- времени, без уравнений Эйнштейна уже не обойтись.
Материальные тела обладают такой характеристикой как масса. Чем массивнее тело, тем труднее столкнуть его с места или поднять. Масса играет в тяготении важнейшую роль, так как она является источником гравитационного поля. И, наоборот, посредством своей массы предмет притягивается другими телами. Масса Солнца действует на массу Земли, притягивая ее. Бывают и сущности без массы, например свет. Но вместо массы свет обладает энергией и импульсом, которые тоже создают гравитационное поле.
Уравнения Эйнштейна состоят из левой и правой частей. Условно говоря, левая их часть соответствует геометрии – искривлению пространства-времени, а правая часть зависит от материи, точнее, от энергий и импульсов частиц и полей. Таким образом, геометрия и материя взаимосвязаны и влияют друг на друга. Материальное содержание говорит о том, как искривляется пространство-время, а геометрия пространства-времени определяет характер движения материальных объектов. Уравнения Эйнштейна управляют гравитацией примерно так же, как конституция и законы управляют жизнью государства.
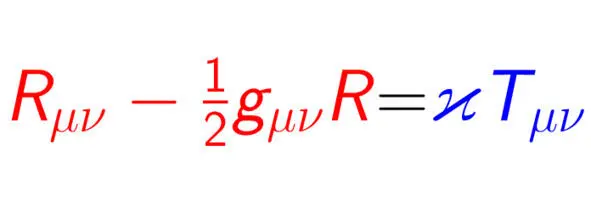
Так выглядят уравнения Эйнштейна
Читать дальше

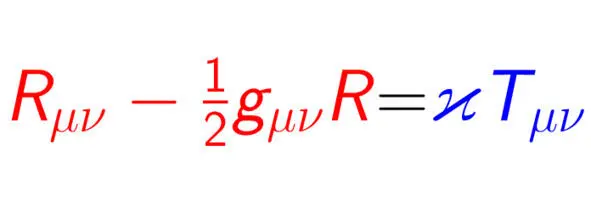





![Стивен Габсер - Маленькая книга о черных дырах [litres]](/books/413500/stiven-gabser-malenkaya-kniga-o-chernyh-dyrah-litr-thumb.webp)
![Стивен Хокинг - Краткая история времени. От Большого взрыва до черных дыр [litres]](/books/416997/stiven-hoking-kratkaya-istoriya-vremeni-ot-bolshogo-thumb.webp)
![Алисия Эванс - Жизнь внутри меня [litres]](/books/435079/alisiya-evans-zhizn-vnutri-menya-litres-thumb.webp)



