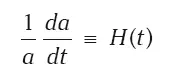Александр Петров - Гравитация. От хрустальных сфер до кротовых нор

Тип пространства определяется плотностью энергии (или, эквивалентно, массы материи) во Вселенной. Плотность, при которой пространство плоское, называют критической. Если плотность материи меньше критической, то пространство Вселенной будет первого типа, если больше – третьего. Более детальное обсуждение типа космологических решений в зависимости от критической плотности приведено в Дополнении 8.

Поскольку мы уже немного владеем понятием метрики, то здесь будет полезным символически представить метрику решений Фридмана:

ds 2= c 2 dt 2– a 2( t ) dl 2.

Здесь единственной информативной переменной оказывается величина a ( t ), которая называется масштабным фактором и показывает, как меняется расстояние между фиксированными частицами в расширяющейся Вселенной. Именно a ( t ) определяет постоянную Хаббла:

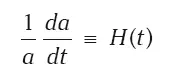
в законе v = Hr. Напомним, что величина H ( t ) медленно меняется со временем и постоянна в каждый момент во всем пространстве.

Итак, для метрики Фридмана уравнения ОТО превращаются просто в уравнения для a ( t ), плотности ρ и давления p материи. Связь между плотностью и давлением задается уравнением состояния. При решении этих уравнений определяется поведение a ( t ) в зависимости от времени. Таким образом, увеличение a ( t ) и означает расширение.

В большой степени на этом уровне для данного типа моделей роль гравитационной теории заканчивается. Далее, в рамках ОТО, самым важным является определение поведения a ( t ), что зависит от динамики материи (наполнителя), ее взаимопревращений. Дальнейшее изложение будет посвящено именно этому.

Существует различие в характере расширения открытых и замкнутых вселенных Фридмана. В первом случае расширение продолжается, хоть и с замедлением, но бесконечно. На рис. 9.3: кривая I – это гипербола и описывает расширение открытого гиперболического мира, кривая II – это парабола и описывает расширение открытого пространственно плоского мира. В третьем случае расширение в определенный момент сменяется сжатием: кривая III на рис. 9.3 иллюстрирует такое поведение.

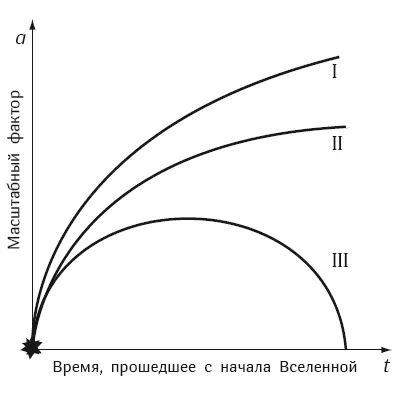
Рис. 9.3. Изменение масштабного фактора

Если представления о бесконечных пространствах обычно не поражают воображение и не требуют пояснений, то таковые необходимы для последнего случая. Свойства 3-мерной сферы напоминают свойства обычной 2-мерной сферы – поверхности шара. Представим путешественника, движущегося по меридиану от Северного полюса к Южному. Миновав Южный полюс, путешественник начнет возвращаться к Северному, но с другой стороны. Точно так же путешественник в «замкнутом мире» 3-мерной сферы, удаляясь от Земли, достигнет полюса мира на 3-мерной сфере, а затем станет возвращаться к Земле, но с другой стороны.

Но что такое полюс (или противоположная точка по отношению к данной) на поверхности Земли – ясно. А что такое полюс 3-мерной сферы? Вот и начнем объяснения с поверхности Земли. Пусть наблюдатель помещен на Северном полюсе Земли. Пусть радиусами (отрезками меридиана, исходящими из полюса) все большей длины он прочерчивает одну за другой концентрические окружности (данной широты). Эти окружности сначала будут увеличиваться, пока не достигнут максимума на экваторе. Затем, с увеличением радиуса, длины этих окружностей начнут уменьшаться! Наконец, когда длина радиуса достигнет полной длины меридиана, длина окружности превратится в ноль! Мы достигнем Южного полюса – противоположного Северному!

Аналогично описывается 3-мерная сфера! Определяя некоторую точку на 3-сфере, как Исходный полюс, и удаляясь от него, исследователь будет описывать концентрические 2-сферы . Сначала площади этих сфер будут увеличиваться, пока не достигнут наибольшей по площади с центром в Исходном полюсе. Эту сферу можно назвать экватором замкнутого 3-мерного мира по отношению к Исходному полюсу. Затем, продвигаясь за экватор, исследователь обнаружит уменьшение (!) площадей 2-сфер. Продвигаясь еще дальше, он максимально удалится от Исходного полюса – там площадь 2-сферы обратится в ноль (!). Это как раз и означает, что он достиг Противоположного полюса.