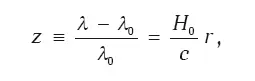Александр Петров - Гравитация. От хрустальных сфер до кротовых нор

Как показали дальнейшие события, Эйнштейн оказался неправ – решения, найденные Фридманом и позднее Леметром, как раз соответствуют реальной физике расширяющейся Вселенной. К сожалению, Фридман умер рано и не успел развить идеи, связанные с его космологическими решениями. Кроме того, он был математиком и не был хорошо знаком, в отличие от Леметра, с данными астрономии. В дальнейшем именно Леметр предложил теоретическое обоснование новых решений как физик, что сделало теорию знаменитой.

Но решающим аргументом стали представленные в 1929 году итоги наблюдений блистательного американского ученого Эдвина Хаббла (1889–1953), рис 9.2. Наблюдая удаленные галактики, он установил следующую закономерность: смещение линий в спектрах удаленных галактик пропорционально расстоянию до них:

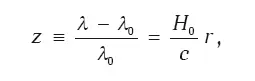
где λ – наблюдаемая длина волны линии, λ 0– длина этой же волны в лаборатории, r – расстояние до галактики, c – скорость света, H 0– постоянная Хаббла, медленно меняющаяся величина, постоянная во всем пространстве на текущую эпоху, z – космологическое красное смещение. Хаббл использовал расстояния до галактик, рассчитанные по видимому блеску цефеид в этих галактиках, собственная светимость которых хорошо известна. В настоящее время способов определения расстояний больше, и закон Хаббла подтверждается для расстояний в миллиарды парсеков. Напомним, что 1 пк (парсек) равен расстоянию до объекта в космосе, параллакс которого с радиуса орбиты Земли равен одной угловой секунде (1 пк = 3,3 св. года).

Рис. 9.2. Эдвин Хаббл

Объясняется космологическое красное смещение эффектом Доплера. Вспомним, что звук приближающегося поезда выше (частота больше), чем звук удаляющегося.

Аналогично звуковым волнам, такой же эффект имеет место и для электромагнитных волн, в частности, для света: от удаляющегося источника приемник зарегистрирует свет меньшей частоты (большей длины волны), чем от лабораторного источника, и большей частоты – от приближающегося. Для скоростей значительно меньше скорости света верна формула Доплера: v = cz. Если сравним ее с законом Хаббла, то придем к выводу, что галактики разбегаются и их скорость увеличивается прямо пропорционально расстоянию. Закон Хаббла перепишется в виде:

v = H 0r,

чем дальше от нас галактика, тем больше ее скорость.

Величина z также очень удобна для оценки возраста объекта, от которого пришел свет. Действительно, z прямо связано с расстоянием, а расстояния – значительные и для их преодоления необходимо значительное время. Поэтому сигнал приносит информацию об объекте на более ранних стадиях расширения. Чем больше z , тем более ранняя эпоха исследуется. Отметим, что для больших z простую формулу Доплера необходимо корректировать с учетом ОТО.

Это открытие заставило раз и навсегда отказаться от понятия статичной Вселенной. Кроме того, предсказанное в решениях Фридмана и Леметра, оно стало еще одним подтверждением правильности новой теории гравитации.

После открытия Хаббла ученые обратили внимание на распределение скоростей, и обнаружили, что оно изотропно, как и полагалось в решениях Фридмана. Это означает, что наблюдатели, помещенные в различные точки пространства, не обнаружат выделенных направлений. Для каждого из них картина распределения скоростей разбегающихся галактик будет выглядеть как для нас: сферически симметричной. Таким образом, предположения Фридмана были сформулированы в виде космологического принципа , согласно которому в больших пространственных масштабах во Вселенной нет выделенных областей и направлений. Большинство специалистов согласно с тем, что любая модель Вселенной должна ему удовлетворять. По современным наблюдательным данным материя во Вселенной распределена однородно и изотропно на масштабах больших 50–100 Мпк.

Существует три типа решений Фридмана. Каждому из них соответствует свой тип геометрии пространства однородной и изотропной Вселенной. Для первого типа – 3-мерное пространство, в котором мы себя ощущаем в каждый момент времени, оказывается бесконечным, безграничным и с отрицательным знаком кривизны. Такие пространства называют гиперболическими, а в решениях Фридмана значение радиуса кривизны увеличивается со временем. Для второго типа решений 3-мерное пространство также оказывается бесконечным и безграничным, но не искривленным; его называют плоским. Первый и второй типы решений называют открытыми. Для третьего типа решений 3-мерное пространство является безграничным, но не бесконечным – его объем конечен. Это пространство с положительным знаком кривизны; его называют замкнутым. В качестве наглядного примера можно привести 2-мерное пространство обычной сферы. Замкнутое пространство можно классифицировать как 3-мерную сферу, экзотические свойства которой мы обсудим ниже. Примеры 2-мерных поверхностей разного типа приведены на рис. 8.6.