Сергей Парновский - Как работает Вселенная - Введение в современную космологию

В частности, если свободно падающий наблюдатель пересекает горизонт событий сверхмассивной черной дыры, он не почувствует ничего особенного. Но не факт, что он сможет долететь в целости до горизонта событий небольшой черной дыры.

Оценим теперь время полета внутри черной дыры – от пересечения горизонта событий до центральной сингулярности. Используем прием, столь любимый физиками-теоретиками, который называется анализом размерности. Так как время падения – кинематическая величина, оно не может зависеть от параметров падающего тела из-за принципа эквивалентности. Таким образом, оно может зависеть только от параметров черной дыры. Черная дыра Шварцшильда имеет только один параметр: массу. У нас также есть две соответствующие фундаментальные константы – гравитационная постоянная G и скорость света в вакууме с. Единственной комбинацией этих трех величин с размерностью времени является GM/c3. Таким образом, время падения в черную дыру будет равно kGM/c3 ≈ 4,93 k M/M☉ мкс, где k – некий безразмерный коэффициент. Мы получили ответ, причем в рамках ОТО, ничего не рассчитывая и не используя никаких формул. В этом состоит прелесть анализа размерности. Тут мы могли бы добавить, что величина k по порядку величины не должна сильно отличаться от единицы.

Чтобы найти ее точное значение, понадобятся и формулы, и расчеты. Величина k зависит от того, как именно тело падает, но она не может превышать π в любом случае, даже если тело – это ракета и она включит свой двигатель, пытаясь изо всех сил затормозить падение. Это предельное значение k = π не может быть получено из нерелятивистских формул; заинтересованных отошлем к задаче 17.3 в книге (Lightman, 1975). Таким образом, максимальное время падения в черную дыру равно πGM/c3 ≈ 15,5 M/M☉ мкс. Для черной дыры в центре нашей Галактики Sagittarius A* это время будет около минуты. Для самой массивной из известных черных дыр, находящейся в галактике NGC 4889, с массой около 21×109 солнечных масс, оно было бы около 90 часов, так что падающий наблюдатель имел бы достаточно времени, чтобы обдумать, было ли его решение прыгнуть в дыру действительно мудрым.

Время падения измеряется в системе падающего наблюдателя, т. е. по его собственным часам. Это уточнение очень важно, так как время, измеренное в разных системах отсчета, т. е. разными наблюдателями, может существенно различаться. Вблизи черной дыры гравитационное поле очень сильно и приводит к замедлению времени, так называемому гравитационному красному смещению.

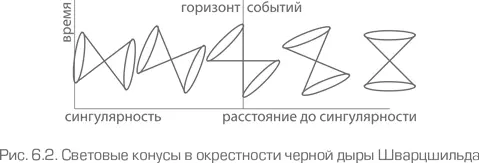
Обратим внимание на то, что к сингулярности тело приближается по времени, роль которого играет координата r. Такая сингулярность называется пространственноподобной. Другими примерами такой сингулярности являются космологические сингулярности, т. е. Большой взрыв, Большой хруст и Большой разрыв. Остальные три координаты, в том числе координата, обозначаемая буквой t, вне черной дыры соответствующая времени, внутри черной дыры пространственноподобны, т. е. вдоль них можно двигаться в любом направлении. Для иллюстрации рассмотрим световые конусы падающего тела, показанные на рис. 6.2. Напомним, что световой конус – это гиперповерхность [91] Гиперповерхность представляет собой трехмерное сечение четырехмерного пространства. в пространстве-времени, которая образуется при прохождении света через определенную точку. Самое главное его свойство – это то, что независимо от того, что делает объект, он не может выйти за пределы своего светового конуса. Более подробная информация приведена в разделе 1.2.8.

Вдали от черной дыры световой конус выглядит вполне нормально: свет распространяется одинаково в любом направлении, поэтому ось светового конуса направлена вдоль оси t. Когда объект приближается к черной дыре, ее гравитация начинает притягивать свет (вспомним гравитационное линзирование). С точки зрения удаленного наблюдателя, свет распространяется быстрее в направлении черной дыры, чем от нее, и световой конус наклоняется в сторону черной дыры. На горизонте событий световой конус наклонен таким образом, что его внешний край проходит параллельно оси t. С этого момента больше невозможно избежать падения в черную дыру. Внутренний край проходит параллельно оси r. Если падающий наблюдатель углубится внутрь черной дыры, его световой конус наклоняется еще сильнее. Теперь оба его края обращены к сингулярности и направлены в противоположных направлениях вдоль оси t. Таким образом, достаточно быстро движущееся тело может двигаться в противоположном направлении оси t, оставаясь внутри своего светового конуса. Возле центральной сингулярности световой конус должен быть повернут на 90°, но эта простая аналогия не очень работает в окрестности сингулярности.