Теоретически, если падающее тело является, скажем, ракетой, оно может включить двигатели и изменить направление своего движения, начав двигаться с увеличением радиальной координаты. По мнению некоторых специалистов, пролетев через внутренний горизонт, оно снова попадает в область, где радиальная координата времениподобна, и теперь будет увеличиваться, т. е. тело окажется внутри белой дыры, через горизонт которой оно и вылетит наружу. А куда, собственно, оно вылетит? Ответа на этот вопрос никто дать не в состоянии. Непонятно ни в какой точке, ни в какой момент времени, ни вообще в какой вселенной это произойдет. Однако любителей путешествия в неизведанное ожидает одна проблема. Внутренний горизонт черной дыры с разумными с астрономической точки зрения параметрами находится слишком близко к сингулярности, и бросившийся в черную дыру будет разорван еще до того, как его пересечет. Более того, сама идея о том, что внутренний горизонт можно пересечь изнутри, является спекулятивной.
6.1.3. Вращающаяся черная дыра Керра
Последний тип черных дыр, которые мы рассмотрим, – это незаряженные, но вращающиеся черные дыры, описываемые метрикой Керра [92] Мы опускаем описание заряженной вращающейся черной дыры Керра — Ньюмена, сочетающей в себе качественные свойства черных дыр Райсснера — Нордстрёма и Керра.
. Так как большинство астрономических объектов вращаются, это, как полагают, наиболее распространенный тип черных дыр. Как и черная дыра Райсснера – Нордстрёма, черная дыра Керра имеет ограничение. Ее момент импульса при заданной массе не должен превышать критического значения, определяемого ее массой.
В этом случае центральная сингулярность будет окружена сферическим горизонтом событий. Вокруг этого горизонта будет располагаться еще одна поверхность, называемая пределом стационарности. Она имеет форму сплюснутого эллипсоида вращения и касается горизонта событий в точках, лежащих на оси вращения. Пространство между двумя этими поверхностями называется эргосферой. Доказано, что любое тело, попавшее в эргосферу, не может быть неподвижно относительно удаленного наблюдателя – оно обязано вращаться в ту же сторону, что и черная дыра. Вращающиеся в эргосфере тела могут иметь отрицательную полную энергию с учетом энергии покоя. Поэтому тело, залетевшее в эргосферу, может распасться на два тела, одно из которых имеет отрицательную энергию, а второе, по закону сохранения энергии, будет иметь большую энергию, чем исходное тело.
Если развивать идею решения энергетическо-экологических проблем при помощи черных дыр, то можно направить в эргосферу черной дыры контейнер с мусором. Часовой механизм в заданное время откроет контейнер и выбросит мусор на орбиту с отрицательной полной энергией. Ускорившийся контейнер вылетит из эргосферы, и его кинетическая энергия может быть использована в интересах народного хозяйства. Таким образом, можно получить энергию, большую чем mc2, где m – масса выброшенного мусора. Откуда же берется дополнительная энергия? Мусор, выброшенный в эргосферу, вращается в сторону, противоположную направлению вращения черной дыры. Провалившись внутрь черной дыры, он уменьшит ее момент импульса. Таким образом, энергия будет получена за счет замедления вращения черной дыры. Такой процесс был предложен Роджером Пенроузом.
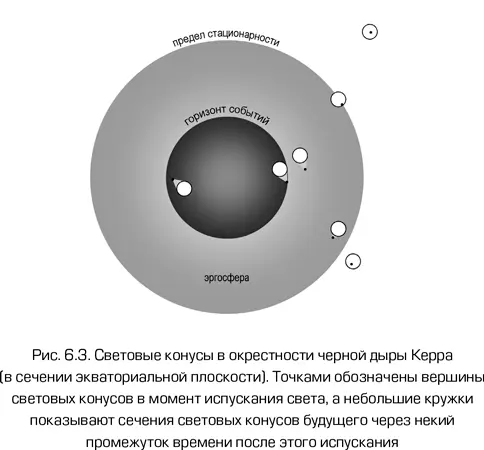
Свойства световых конусов вблизи черной дыры Керра показаны на рис. 6.3. В отличие от сферически-симметричной черной дыры Шварцшильда, черная дыра Керра имеет избранное пространственное направление – ее ось вращения и направление этого вращения. Пространство вокруг черной дыры Керра тоже затягивается в это вращение. Поэтому световые конусы наклоняются не только к центру, но и в направлении вращения. Мы не можем изобразить их на двумерном рисунке, как мы делали это на рис. 6.2 для шварцшильдовской дыры, отказавшись от явного изображения оси времени. По этой причине на рис. 6.3 мы изображаем экваториальное сечение черной дыры Керра, помещаем туда некоторое количество пробных частиц (черных точек), каждая из которых синхронно вспыхивает, становясь вершиной своего светового конуса. Свет от каждой вспышки расходится в стороны, образуя расширяющуюся оболочку или фронт разбегающейся волны. Через некоторое время (в системе отсчета удаленного наблюдателя) мы фиксируем круги, образованные пересечением экваториальной плоскости и фронтов этих волн, как границы белых кружков, изображенных на рис. 6.3. Самая близкая аналогия – водоворот, на который смотрят сверху. В него бросают камешки и наблюдают, как от места падения расходятся круги на поверхности воды.
Читать дальше
Конец ознакомительного отрывка
Купить книгу



![Сергей Скиба - Лиганец (СИ) [Вселенная EVE-online]](/books/25287/sergej-skiba-liganec-si-vselennaya-eve-online-thumb.webp)







