Сергей Парновский - Как работает Вселенная - Введение в современную космологию

В этом разделе мы определяем, сколько времени осталось существовать нашей Вселенной, если она имеет какую-то темную энергию с w < –1, которая также называется фантомной энергией.

Судьба нашей Вселенной – вопрос очень серьезный, поэтому давайте оценим, сколько времени у нас осталось. Мы можем забыть про все остальное, кроме фантомной энергии, потому что за конечное время она будет доминировать и определять скорость расширения Вселенной. В этом случае постоянная Хаббла будет увеличиваться по степенному закону: H ~ rα, где α = –3(1 + w)/2 > 0. Если рассматривать зависимость скалярного фактора от времени, то мы получим r ~ (t0 – t)–1/α, где время t0 соответствует моменту Большого разрыва. Таким образом, Вселенная вырастет до бесконечного размера за конечное время.

Из обобщения уравнения (A.10) в присутствии фантомной энергии мы можем получить уравнение для скорости изменения скалярного фактора. Используя текущие значения Ωm0 и ΩDE0 – параметр плотности материи и фантомной энергии [85] В качестве приближенной величины для ΩDE0 мы использовали текущее значение ΩΛ0, взятое из ΛCDM-модели. , которая, как мы предполагаем, имеет уравнение состояния (2.33) с w < –1, мы можем определить время до Большого разрыва:

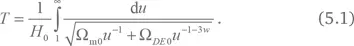
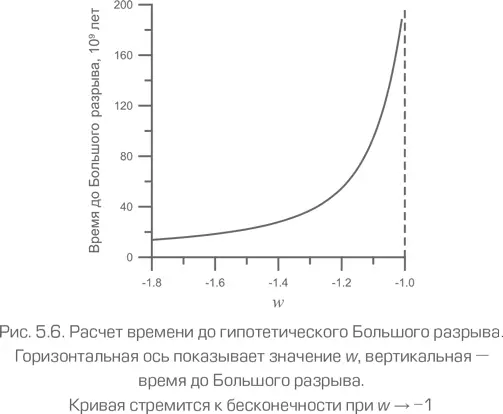
На рис. 5.6 показан график зависимости времени до Большого разрыва от величины параметра w. В соответствии с ограничениями по данным различных астрономических наблюдений, приведенными на рис. 5.4, она не может быть меньше чем –1,2, а это значит, что Большой разрыв произойдет не раньше чем через 55 млрд лет с 99 %-ной вероятностью. Так что угроза Большого разрыва – самая незначительная из проблем, стоящих перед человечеством.

Тем не менее Вселенная содержит не только космологическую постоянную и холодную темную материю. Существует много электромагнитного излучения с параметром w = 1/3 в формуле (2.34). Его плотность зависит от красного смещения, как (1 + z)4. Таким образом, если мы путешествуем в прошлое, космологическая константа будет иметь постоянную плотность, плотность пылевой материи будет возрастать как (1 + z)3, а плотность излучения – как (1 + z)4. Плотность излучения будет превалировать в очень ранней Вселенной. При z ≈ 3200 плотности излучения и вещества были равны, затем доминировала пылевидная материя. То же самое уравнение состояния мы можем использовать для нейтрино, которые являются ультрарелятивистскими частицами с очень малой массой покоя. Их можно рассматривать как небарионную, так называемую горячую материю из-за их скоростей, близких к скорости света. Их плотность падает быстрее, чем плотность холодной материи.

Уравнения (2.12) и (2.13) легко могут быть обобщены на случай наличия некоторых других видов материи с уравнением состояния (2.33). Может ли добавление этих новых видов материи кардинально повлиять на ход эволюции Вселенной? Да, если среди них есть так называемая фантомная материя или фантомная энергия с уравнением состояния вида (2.33) с w < –1.

Действительно, если при расширении Вселенной не будет материи с возрастающей плотностью, то постоянная Хаббла будет стремиться к некоему постоянному значению. Это означает экспоненциальный рост Вселенной. Но присутствие фантомной материи все изменит. Ее плотность будет увеличиваться с течением времени. В результате мы придем к так называемому Большому разрыву: это другой вид конца света, которым закончится судьба нашей Вселенной. В этом случае скорость расширения будет неограниченно возрастать, и все тела будут разорваны на куски, затем молекулы, атомы и элементарные частицы. Мы уже говорили об этом в разделе 5.2.

Выполним наше обещание и расскажем о некоторых экзотических объектах, предсказанных ОТО. Они существенно менее распространены, чем темная материя или темная энергия, однако достаточно интересны, чтобы быть по крайней мере упомянутыми в этой книге.

Первый тип объектов, которые мы рассмотрим, – черные дыры, многие из которых наблюдались астрономами. Черная дыра представляет собой объект с плотностью настолько высокой, что пространственная кривизна и приливные силы в ее центре становятся бесконечными (это называется «пространственно-временная сингулярность», или просто «особенность» для краткости). Эта особенность окружена горизонтом событий – «поверхностью» черной дыры. Любой объект, включая свет, проваливается внутрь дыры через ее горизонт событий, но не может покинуть ее и должен двигаться в направлении центральной сингулярности. Именно поэтому этот объект называют черной дырой.