Некоторые из этих примеров перечислены более подробно в Letkowski, J. 2012. Applications of the Poisson probability distribution.
Tomasetti, C. & Vogelstein, B. Variation in cancer risk among tissues can be explained by the number of stem cell divisions. – Science 347(6217), 2015. – p. 78–81.
В этой модели я использую четыре параметра для каждой команды: среднее число забитых голов дома (SH), пропущенных дома(CH), забитых(SA) и пропущенных(CA) на выезде. Они оцениваются по голам, забитым в сезоне-2012/13. Когда две команды встречаются в лиге в моем моделированном сезоне-2013/14, я сначала генерирую цели для хозяев. Они распределены по Пуассону со средним значением, равным 1/2 (SH + CA), которое учитывает атакующую силу хозяев и оборону гостей. Голы гостей распределены по Пуассону со средним значением, равным 1/2 (CH + SA). Чтобы получить полный сезон, процедура повторяется для всех матчей.
ТВ-программа о футболе. Выходит каждую субботу на BBC.
Для соединения всех 11 игроков требуется не менее 10 связей между игроками. Сеть, соединяющая всех игроков вместе, используя ровно 10 ссылок, называется остовным деревом. Чтобы построить показанную сеть, я сначала нахожу остовное дерево с наименьшей общей длиной – минимальное остовное дерево. На втором этапе я вычисляю новое минимальное остовное дерево, которое не содержит ссылок от первого остовного дерева. Показанная сеть объединяет эти деревья.
Используемые здесь позиции адаптированы из книги Джонатана Уилсона «Переворачивая пирамиду: История футбольной тактики» (Orion Books, Лондон, 2008). Книга охватывает эти и многие другие формации, используемые в истории футбола.
Длина каждой из четырех ветвей, соединенных с пригородами, равна 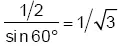 Применяя теорему Пифагора, средняя длина тогда
Применяя теорему Пифагора, средняя длина тогда 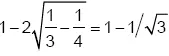 . Общая сумма равна
. Общая сумма равна 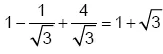 .
.
Tero, A. Rules for biologically inspired adaptive network design. – Science 327(5964), 2010. – p. 439–442.
Зоны, которые я вычисляю здесь, как я объясню ниже в основном тексте, представляют собой наборы точек, наиболее близкие к каждому игроку. Таким образом, все точки в игровых зонах – это те, которые ближе к этому игроку, и никакому другому. Это разбиение известно как диаграмма Вороного, в честь украинского математика Георгия Вороного.
Для вычисления триангуляции сначала используем диаграмму Вороного для расчета зон. Затем мы берем центральные точки всех зон диаграммы Вороного (то есть игроков) и рисуем связи между ними, если они имеют соседние зоны, чтобы создать триангуляцию Делоне. Для сети «Барселоны» первое и второе минимальное остовное дерево содержат большинство краев триангуляции Делоне. Триангуляции Делоне имеют тенденцию максимизировать углы в соединительных сетях, а диаграмма Вороного максимизирует размеры зон. Мы можем переключать взаимозаменяемость между двумя: каждая диаграмма Вороного имеет эквивалентную триангуляцию Делоне, и наоборот. Поэтому, когда мы максимизируем углы, мы максимизируем зоны, и наоборот.
Испанец равноудален от всех защитников, которые находятся поблизости ( прим. пер. ).
Для обзора см. Sumpter, D. J. The modelling cycle for collective animal behaviour. – Interface Focus 2(6), 2012. – p. 764–773.
Alvarez, G. A. & Franconeri, S. L. How many objects can you track? Evidence for a resource-limited attentive tracking mechanism. – Journal of Vision 7(13) – п. 14.1–14.10.
Michels, R. 2001. Teambuilding: The Road to Success – Reedswain Publishing, Spring City, PA, 2001. – p. 88
Техническая часть работы была выполнена Эмилем Розеном, студентом магистратуры моей исследовательской группы. Эмиль продолжил писать диссертацию, изучающую модели движения моей команды.
Moussaïd, M. Experimental study of the behav-ioural mechanisms underlying self-organization in humancrowds. – Proceedings of the Royal Society B: Biological Sciences. DoI: 10.1098/rspb.2009.0405.
Стрелки на рисунке 3.4 показывают только эффект неподвижного студента, а не общую тенденцию движущегося студента. В пустом коридоре движущийся студент идет вперед с относительно постоянной скоростью. Чтобы создать рисунок, это движение вперед в отсутствие неподвижного студента вычитается из движения, измеряемого в присутствии неподвижного студента, что и дает общий эффект.
Читать дальше

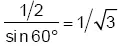 Применяя теорему Пифагора, средняя длина тогда
Применяя теорему Пифагора, средняя длина тогда 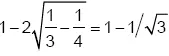 . Общая сумма равна
. Общая сумма равна 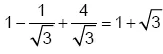 .
.










