Макс Тегмарк - Жизнь 3.0. Быть человеком в эпоху искусственного интеллекта

Мы приблизились к возможному ответу на наш исходный вопрос о том, как грубая физическая материя может породить нечто представляющееся настолько эфемерным, абстрактным и бестелесным, как разум: он кажется нам таким бестелесным из-за своей субстрат-независимости, из-за того, что живет своей жизнью, которая не зависит от физических деталей его устройства и не отражает их. Говоря коротко, вычисление – это определенная фигура пространственно-временного упорядочения атомов, и важны здесь не сами атомы, а именно эта фигура! Материя не важна.

Другими словами, “хард” здесь материя, а фигура – это “софт”. Субстрат-независимость вычисления означает, что AI возможен: разум не требует ни плоти, ни крови, ни атомов углерода.

Благодаря этой субстрат-независимости изобретательные инженеры непрерывно сменяют одну технологию внутри компьютера другой, радикально улучшенной, но не требовавшей замены “софта”. Результат во всех отношениях нагляден в истории запоминающих устройств. Как показывает рис. 2.8, стоимость вычисления сокращается вдвое примерно каждые два года, и этот тренд сохраняется уже более века, снизив стоимость компьютера в миллион миллионов миллионов (в 10 18) раз со времен младенчества моей бабушки. Если бы все сейчас стало в миллион миллионов миллионов раз дешевле, то сотой части цента хватило бы, чтобы скупить все товары и услуги, произведенные или оказанные на Земле в тот год. Такое сильное снижение цены отчасти объясняет, почему сейчас вычисления проникают у нас повсюду, переместившись из отдельно стоящих зданий, занятых вычисляющими устройствами, в наши дома, автомобили и карманы – и даже вдруг оказываясь в самых неожиданных местах, например в кроссовках.

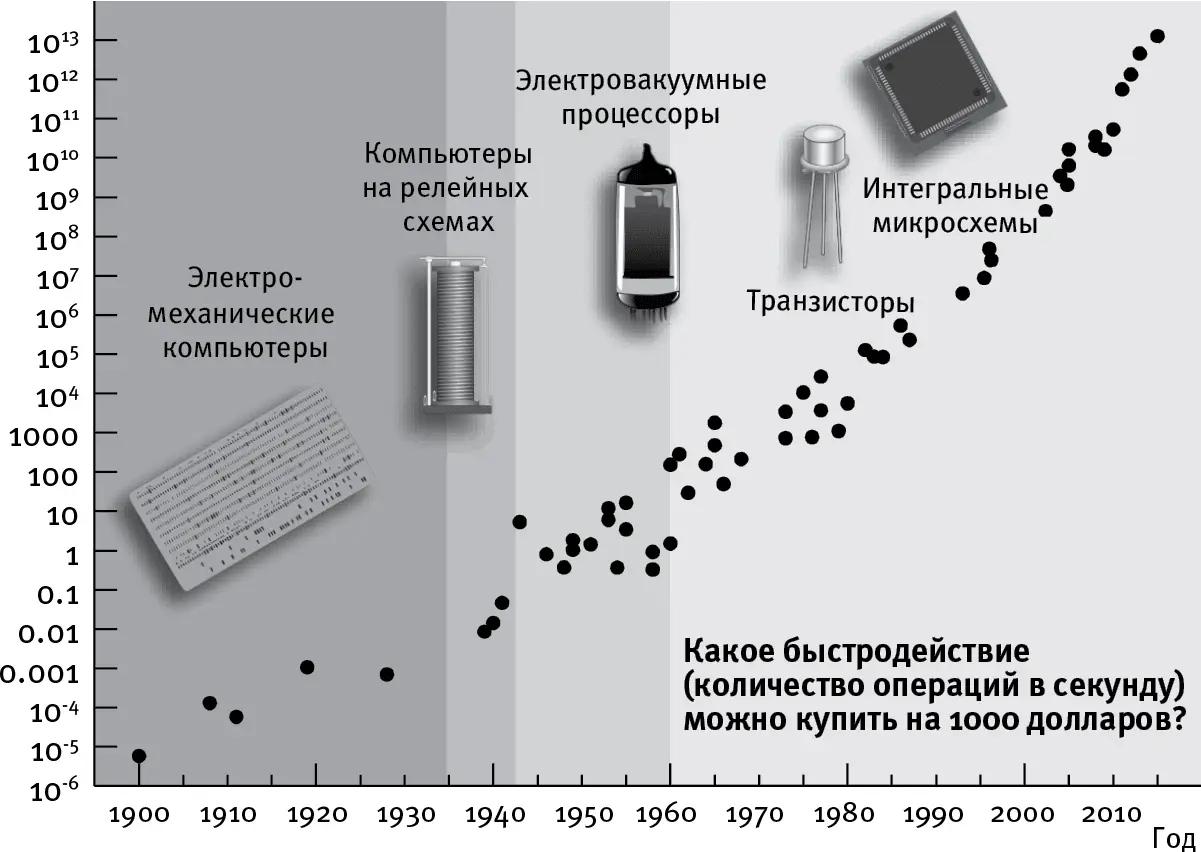
Рис. 2.8

С 1900 года вычисления становились вдвое дешевле примерно каждые пару лет. График показывает, какую вычислительную мощность, измеряемую в количестве операций над числами с плавающей запятой в секунду (FLOPS), можно было купить на тысячу долларов {5} 5 Данные о стоимости вычислений в разные годы до 2011 взяты из книги Рэя Курцвейла How to Create a Mind, последующие данные вычислены на основании информации, приведенной в: https://en.wikipedia.org/wiki/FLOPS . Частные случаи вычислений, которые соответствуют одной операции над числами с плавающей запятой, соответствуют 10 5элементарным логическим операциям вроде обращения бита (замены 0 на 1, и наоборот) или одного срабатывания гейта NAND.

Почему развитие наших технологий позволяет им удваивать производительность с такой регулярной периодичностью, обнаруживая то, что математики называют экспоненциальным ростом? Почему это сказывается не только на миниатюризации транзисторов (тренд, известный как закон Мура), но, и даже в большей степени, на развитии вычислений в целом (рис. 2.8), памяти (рис. 2.4), на море других технологий, от секвенирования генома до томографии головного мозга? Рэй Курцвейл называет это явление регулярного удвоения “законом ускоряющегося возврата”.

В известных мне примерах регулярного удвоения в природных явлениях обнаруживается та же самая фундаментальная причина, и в том, что нечто подобное происходит в технике, нет ничего исключительного: и тут следующий шаг создается предыдущим. Например, вам самим приходилось переживать экспоненциальный рост сразу после того, как вас зачали: каждая из ваших клеточек, грубо говоря, ежедневно делится на две, из-за чего их общее количество возрастает день за днем в пропорции 1, 2, 4, 8, 16 и так далее. В соответствии с наиболее распространенной теорией нашего космического происхождения, известной как теория инфляции , наша Вселенная в своем младенчестве росла по тому же экспоненциальному закону, что и вы сами, удваивая свой размер за равные промежутки времени до тех пор, пока из крупинки меньше любого атома не превратилась в пространство, включающее все когда-либо виденные нами галактики. И опять причина этого заключалась в том, что каждый шаг, удваивающий ее размер, служил основанием для совершения следующего. Теперь по тому же закону стала развиваться и технология: как только предыдущая технология становится вдвое мощнее, ее можно использовать для создания новой технологии, которая также окажется вдвое мощнее предыдущей, запуская механизм повторяющихся удвоений в духе закона Мура.

Но с той же регулярностью, как сами удвоения, высказываются опасения, что удвоения подходят к концу. Да, действие закона Мура рано или поздно прекратится: у миниатюризации транзистора есть физический предел. Но некоторые люди думают, что закон Мура синонимичен регулярному удвоению нашей технической мощи вообще. В противоположность им Рэй Курцвейл указывает, что закон Мура – это проявление не первой, а пятой технологической парадигмы, переносящей экспоненциальный рост в сферу вычислительных технологий, как показано на рис. 2.8: как только предыдущая технология перестает совершенствоваться, мы заменяем ее лучшей. Когда мы не можем больше уменьшать вакуумные колбы, мы заменяем их полупроводниковыми транзисторами, а потом и интегральными схемами, где электроны движутся в двух измерениях. Когда и эта технология достигнет своего предела, мы уже представляем, куда двинуться дальше: например, создавать трехмерные интегральные цепи или делать ставку на что-то отличное от электронов.