Макс Тегмарк - Жизнь 3.0. Быть человеком в эпоху искусственного интеллекта

Мы можем схематически изобразить нейронную сеть в виде точек, представляющих нейроны, и соединяющих их линий, которые представляют синапсы (см. рис. 2.9). Настоящие синапсы – это довольно сложные электрохимические устройства, совсем не похожие на эту схематическую иллюстрацию: они включают в себя разные части, которые называют аксонами и дендритами; есть много разновидностей нейронов, которые действуют по-разному, и точные детали того, как и когда электрическая активность в одном нейроне влияет на другие нейроны, все еще остаются предметом дальнейших исследований. Однако уже сейчас ясно, что нейронные сети могут достичь производительности человеческого уровня во многих удивительно сложных задачах, даже если на время забыть обо всех этих сложностях и заменить настоящие биологические нейроны чрезвычайно простыми имитирующими их устройствами, совершенно одинаковыми и подчиняющимися очень простым правилам. В настоящее время наиболее популярная модель такой искусственной нейронной сети представляет состояние каждого нейрона одним числом и силу каждого синапса – тоже одним числом. В этой модели при каждом действии каждый нейрон обновляет свое состояние, вычисляя среднее арифметическое от состояния всех присоединенных к нему нейронов с весами, в качестве которых берутся силы их синаптической связи. Иногда еще прибавляется константа, а к результату применяется так называемая функция активации , дающая число, которым будет выступать в качестве состояния данного нейрона на следующем такте [15] Добавим для тех, кто любит математику, что в качестве этой функции чаще всего выступает либо сигмоидальная функция σ ( x ) – 1/(1 + e – x ), либо пороговая функция σ ( x ) = max{0, x }, хотя доказано, что в этой роли можно использовать какую угодно, лишь бы она не была линейной (то есть не представлялась в виде прямой линии на графике). В знаменитой модели Хопфилда использовалась функция σ ( x ) = –1 if x < 0 and σ ( x ) = 1 if x ≥ 0. Если состояния нейронов хранятся в памяти в виде вектора, то при переходе к следующему такту он обновляется умножением сначала этого вектора на матрицу, элементами которой служат силы синаптических связей, и последующим применением функции ⌠(x) ко всем новым вычисленным элементам. . Самый простой способ использовать нейронную сеть как функцию заключается в том, чтобы сделать ее прямой, превратив в канал передачи, где информация направляется лишь в одну сторону, как показано на рис. 2.9, загружая на вход функции верхний слой нейронов и считывая выход со слоя нейронов внизу.

Успешное использование этой простой нейронной сети представляет нам еще один пример независимости от субстрата: нейронная сеть обладает колоссальной вычислительной силой, которая, вне всякого сомнения, не зависит от мелких подробностей в ее устройстве. В 1989 году Джордж Цибенко, Курт Хорник, Максвелл Стинчкомб и Халберт Уайт доказали нечто замечательное: простые нейронные сети вроде только что описанной универсальны в том смысле, что они могут вычислять любую функцию с произвольной точностью, просто приписывая соответствующие значения числам, которыми характеризуются силы синаптических связей. Другими словами, эволюция, вероятно, сделала наши биологические нейроны такими сложными не потому, что это было необходимо, а потому, что это было более эффективно, и потому, что эволюция, в отличие от инженеров-людей, не получает наград за простоту и понятность предлагаемых конструкций.

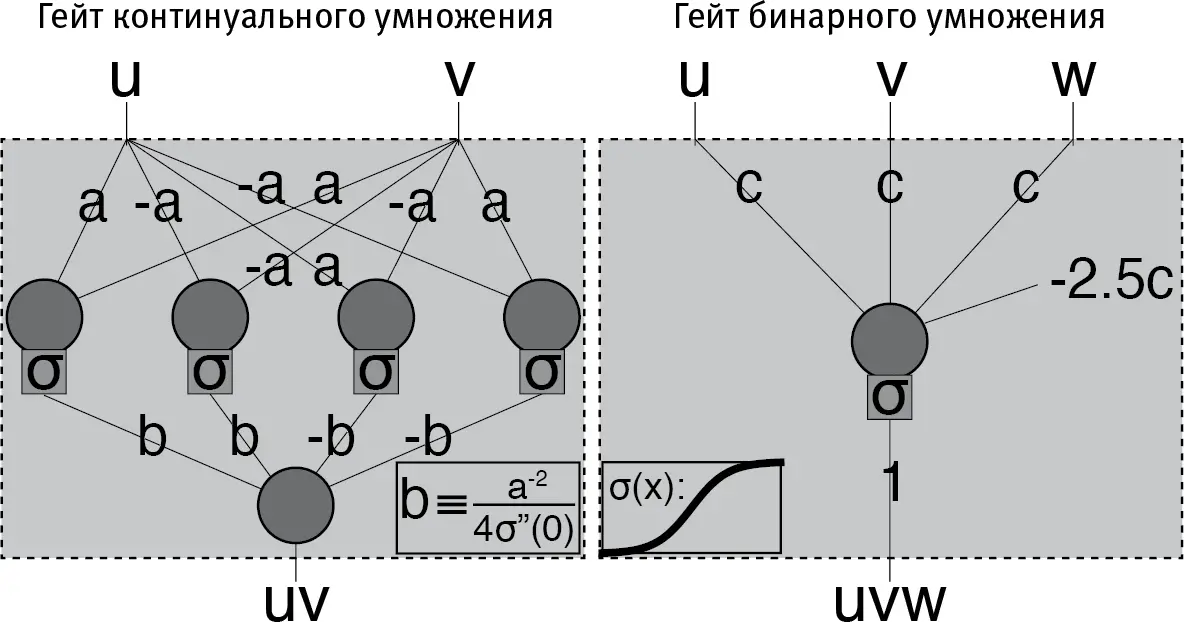
Рис. 2.10

Вещество может производить умножение, используя не гейты NAND, как на рис. 2.7, а нейроны. Для понимания ключевого момента здесь не требуется вникать в детали, достаточно только отдавать себе отчет, что нейроны (как биологические, так и искусственные) не только способны производить математические действия, но их для этого требуется значительно меньше, чем гейтов NAND. Вот еще факультативные детали для упертых фанатов математики : кружочками обозначено сложение, квадратики обозначают применение функции σ , а прямые отрезки – умножение на число, которое этот отрезок пересекает. На входе – вещественное число (слева) или бит (справа). Умножение становится сколь угодно точным при а → 0 (слева) и при с → ∞ (справа). Левая сеть работает при любой функции σ ( х ), имеющей изгиб в нуле σ ”(0) ≠ 0), что можно доказать разложением функции σ ( х ) по формуле Тейлора. Для сети справа надо, чтобы функция σ ( х ) стремилась к нулю и к единице при очень малых и очень больших х соответственно, так чтобы соблюдалось условие uvw = 1, только когда u + v + w = 3 . (Эти примеры взяты из статьи моего студента Генри Лина: https://arxiv.org/abs/1608.08225, проверена 18 мая 2018.) Комбинируя умножения и сложения, можно вычислять любые полиномы, с помощью которых, как известно, мы можем получить апроксимацию любой гладкой функции.