Чарльз Петцольд - Код. Тайный язык информатики

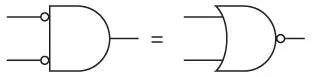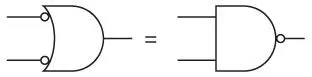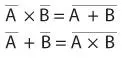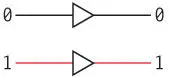
Однако вы можете использовать буфер при наличии слабого входного сигнала. Как вы помните, именно по этой причине реле использовались в телеграфной системе много лет назад. Кроме того, буфер можно применять для небольшой задержки сигнала. Дело в том, что для срабатывания реле требуется немного времени — небольшая доля секунды.

Отныне в книге редко будут встречаться изображения реле. Вместо этого следующие схемы будут состоять из буферов, инверторов, четырех основных логических вентилей и более сложных схем (дешифратора «2 на 4», например), собранных из этих вентилей. Разумеется, все эти компоненты состоят из реле, однако нам нет необходимости их рассматривать.

Ранее, когда мы конструировали дешифратор «2 на 4», нам встретилась небольшая схема следующего типа.

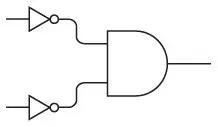
Два инвертированных входа стали входами вентиля И. Иногда такая конфигурация изображается без инверторов.

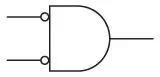
Обратите внимание на маленькие кружки на входе вентиля И, которые указывают, что сигналы в этой точке инвертируются: 0 (отсутствие напряжения) становится 1 (наличие напряжения), и наоборот.

Вентиль И с двумя инвертированными входами ведет себя точно так же, как вентиль ИЛИ-НЕ.

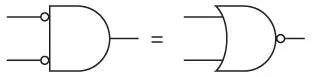
Выход равен 1, только если оба входа равны 0.

Аналогично вентиль ИЛИ с двумя инвертированными входами эквивалентен вентилю И-НЕ.

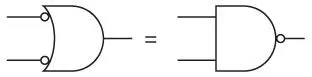
Выход равен 0, только если оба входа равны 1.

Эти две пары эквивалентных схем представляют электрическое воплощение законов Огастеса де Моргана, еще одного математика викторианской эпохи, который был на девять лет старше Буля. Его книга «Формальная логика» была опубликована в 1847 году, согласно преданию, в один день с книгой Буля «Математический анализ логики». На самом деле на занятия логикой Буля подвигла открытая вражда между де Морганом и другим британским математиком, связанная с обвинениями в плагиате (история оправдала де Моргана). С самого начала де Морган осознал важность прозрений Буля. Он бескорыстно поощрял Буля и помогал ему в исследованиях, однако сегодня он, к сожалению, почти забыт, а в памяти потомков остались только его знаменитые законы.

Законы де Моргана проще всего выразить следующим образом.

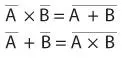
A и B — два булевых операнда. В первом выражении они инвертируются, а затем объединяются с помощью булева оператора И. Это эквивалентно объединению двух операндов с помощью булева оператора ИЛИ и последующему инвертированию результата (соответствует оператору ИЛИ-НЕ). Во втором выражении два оператора инвертируются, а затем объединяются с помощью булева оператора ИЛИ. Это эквивалентно объединению двух операндов с помощью булева оператора И и последующему инвертированию результата (соответствует оператору И-НЕ).

Законы де Моргана — важный инструмент для упрощения булевых выражений, а значит, для упрощения схем. История показала, что именно в этом заключалось значение работы Клода Шеннона для инженеров-электриков. Однако чрезмерное упрощение схем не является целью этой книги. Нам важно собрать работающую схему, а не сделать так, чтобы она работала как можно проще. Этим мы и займемся в следующей главе — соберем работающую счетную машину.

Сложение — простейшая арифметическая операция. Если мы хотим создать компьютер (а именно в этом заключается цель этой книги), сначала нужно найти способ создания устройства, складывающего два числа. По сути, компьютеры выполняют только операцию сложения. Если нам удастся сконструировать механизм, умеющий складывать, мы окажемся способны создать устройство, использующее операцию сложения для того, чтобы вычитать, умножать, делить, рассчитывать платежи по ипотеке, отправлять ракеты на Марс, играть в шахматы и вносить путаницу в наши телефонные счета.