Используя понятия функций распределения, легко получить выражения для вероятностей того, что результат наблюдений Х или случайная погрешность δ примет при проведении измерения некоторое значение в интервале [ x 1, x 2] или [δ 1, δ 2].
В терминах интегральной функции распределения имеем:
P ( x 1 < X ≤ x 2) = P {-∞ < X ≤ x 2} – P{-∞ < X ≤ x 1} = F x ( x 2) – F x ( x 1)
P (δ 1 < δ ≤ δ 2) = P {-∞ < δ ≤ δ 2} – P{-∞ < δ ≤ δ 1} = F δ(δ 2) – F δ(δ 1)
т.е. вероятность попадания результата наблюдений или случайной погрешности в заданный интервал равна разности значений функции распределения на границах этого интервала.
Заменяя в полученных формулах интегральные функции распределения на соответствующие плотности распределения вероятностей согласно выражению (7), получим формулы для искомой вероятности в терминах дифференциальной функции распределения:
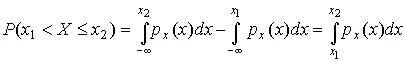 (8)
(8)
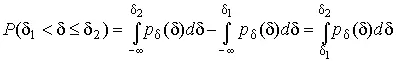 (9)
(9)
Таким образом, вероятность попадания результата наблюдения или случайной погрешности в заданный полуоткрытый интервал равна площади, ограниченной кривой распределения, осью абсцисс и перпендикулярами к ней на границах этого интервала. Необходимо отметить, что результаты наблюдений в значительной степени сконцентрированы вокруг истинного значения измеряемой величины и по мере приближения к нему элементы вероятности их появления возрастают. Это дает основание принять за оценку истинного значения измеряемой величины координату центра тяжести фигуры, образованной осью абсцисс и кривой распределения, и называемую математическим ожиданием результатов наблюдений :
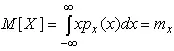 (10)
(10)
В заключение можно дать более строгое определение постоянной систематической и случайной погрешностей.
Систематической постоянной погрешностью называется отклонение математического ожидания результатов наблюдений от истинного значения измеряемой величины:
θ = M [ X ] – Q (11)
а случайной погрешностью — разность между результатом единичного наблюдения и математическим ожиданием результатов
δ = X – M[ X ] (12)
В этих обозначениях истинное значение измеряемой величины составляет
Q = X – θ – δ (13)
4.3. Моменты случайных погрешностей
Функция распределения является самым универсальным способом описания поведения случайных погрешностей. Однако для определения функций распределения необходимо проведение весьма кропотливых научных исследований и обширных вычислительных работ. Поэтому к такому способу описания случайных погрешностей прибегают иногда при исследовании принципиально новых мер и измерительных приборов.
Значительно чаще бывает достаточно охарактеризовать случайные погрешности с помощью ограниченного числа специальных величин, называемых моментами [3].
Начальным моментом n -го порядка результатов наблюдений называется интеграл вида
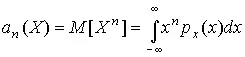 (14)
(14)
представляющий собой математическое ожидание степени X n .
При n =1
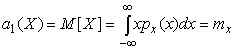 (15)
(15)
т.е. первый начальный момент совпадает с математическим ожиданием результатов измерений.
Центральным моментом n -го порядка результатов наблюдений называется интеграл вида
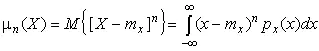 (16)
(16)
Вычислим первый центральный момент:
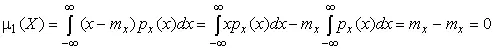 (17)
(17)
Таким образом, первый центральный момент результатов наблюдений равен нулю. Важно отметить, что начальные и центральные моменты случайных погрешностей совпадают между собой и с центральными моментами результатов наблюдений, поскольку математическое ожидание случайных погрешностей равно нулю.
Особое значение наряду с математическим ожиданием результатов наблюдений имеет второй центральный момент, называемый дисперсией результатов наблюдений .
Читать дальше

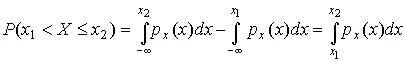 (8)
(8)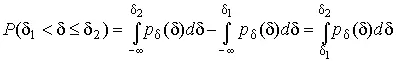 (9)
(9)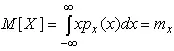 (10)
(10)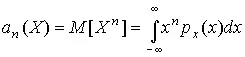 (14)
(14)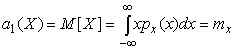 (15)
(15)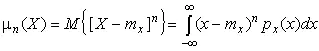 (16)
(16)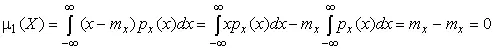 (17)
(17)





