Георгий Горшков - Строение земного шара

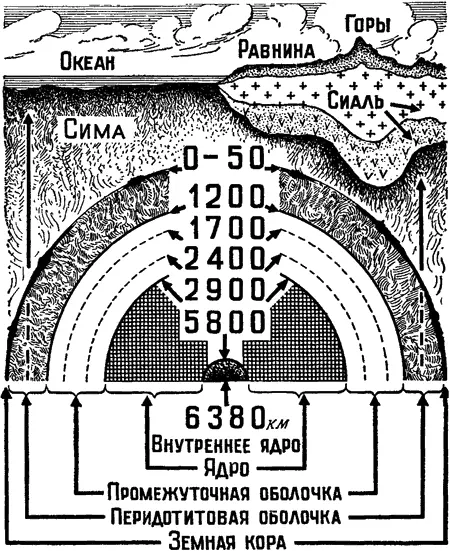
Рис. 7. Строение земного шара.

В последнее время появляются основания говорить о наличии еще нескольких поверхностей раздела (кроме уже упомянутых) на глубинах 900, 1800, 5800 км и др. Наличие подобных границ, или, по крайней мере, основных из них, таких, как подошва сиалической оболочки или граница ядра, сомнений не вызывает. Что же касается соображений о минералогическом составе оболочек и их агрегатном состоянии, то здесь, к сожалению, еще слишком много неясного. Прежде всего, нам мало известно, как изменяется внутри Земли температура и как влияет на свойства вещества одновременное воздействие высокой температуры и высокого давления.

Перейдем к рассмотрению этих вопросов.

Чтобы рассчитать, каких значений достигает давление внутри Земли, вызванное весом горных пород, слагающих различные оболочки, нужно знать плотность пород на всех глубинах и величину силы тяжести также на всех глубинах вплоть до центра.

Как мы видели, плотность пород с глубиною растет, хотя и неравномерно. От 2,5 на поверхности она доходит до 3,4 на глубине около 100 км и до 6,0 на уровне 2900 км ниже поверхности. Здесь, на границе ядра, в величине плотности наблюдается скачок: она сразу достигает значения 9,5 (приблизительно), а далее снова растет равномерно, доходя в центре ядра до 12,5 (по М. С. Молоденскому, 1955) (см. рис. 8).

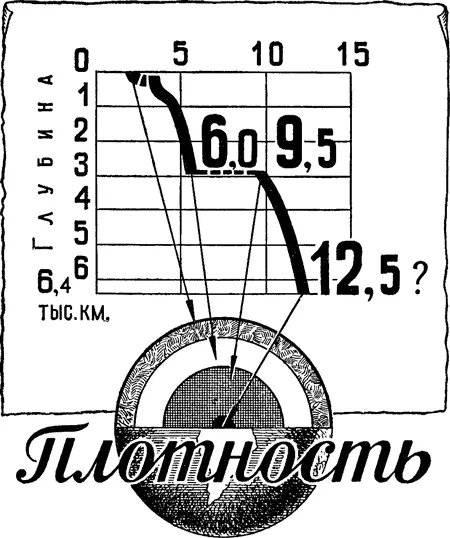
Рис. 8. Изменение плотности внутри Земли.

Что касается силы тяжести, то о ней можно сказать следующее. Сила тяжести — сила, с которой Земля притягивает к себе все тела. Под влиянием этой силы тела, находящиеся в свободном состоянии (например, в воздухе), падают на Землю, т. е. движутся по направлению к центру Земли, постепенно убыстряясь, т. е. получая «ускорение». Величину «ускорения силы тяжести» можно вычислить. На поверхности Земли ускорение силы тяжести равно приблизительно 9,8 м/сек 2 ; в глубине Земли оно сначала немного возрастает, достигая максимума близ поверхности ядра, а затем быстро падает, доходя в центре Земли до нуля (рис. 9). Это понятно: точка, находящаяся в центре земного шара, притягивается всеми окружающими ее частями, с одинаковой силой по всем радиусам, а в итоге равнодействующая будет равна нулю.

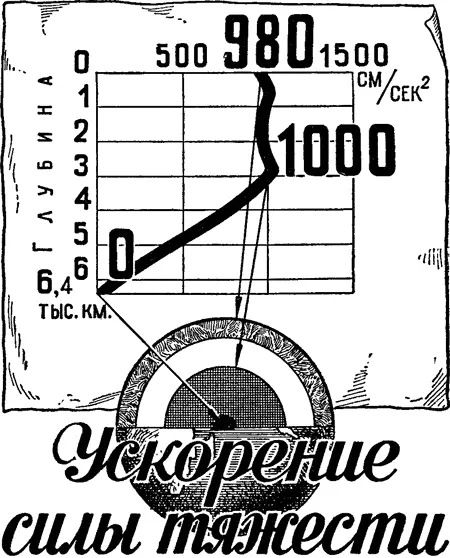
Рис. 9. Изменение ускорения силы тяжести внутри Земли.

Обладая указанными сведениями, мы можем вычислить вес столбика пород с поперечным сечением, равным 1 кв. сантиметру, и длиной, равной радиусу Земли или любой его части. Это и будет давление, оказываемое весом вышележащих пород на элементарную площадку (1 кв. см )в глубине Земли. Расчеты приводят к следующим цифрам: у «подошвы» земной коры, т. е. у основания сиалической оболочки (на глубине 50 км ) — около 13 тыс. атмосфер, т. е. около 13 тонн на квадратный сантиметр; на границе ядра — около 1,4 миллиона атмосфер; в центре Земли — около 3 млн. атмосфер (рис. 10). Три миллиона атмосфер — это приблизительно три тысячи тонн на квадратный сантиметр. Это — огромная величина. Ни в одной лаборатории достичь таких давлений пока не удалось.

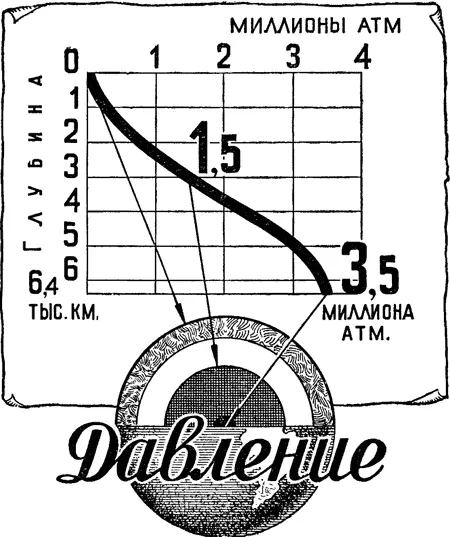
Рис. 10. Изменения давления внутри Земли.

Перейдем к температуре. По данным измерений в буровых скважинах, а также в шахтах, выяснено, что с глубиной температура растет, поднимаясь приблизительно на 3° на протяжении каждых 100 метров. Подобный темп роста температуры сохраняется всюду, на всех материках, но лишь в наружных частях Земли, близ самой ее поверхности. С глубиной величина «геотермического градиента» (геотермический градиент — изменение температуры в градусах на каждый сантиметр) падает. Вычисления, основанные на учете теплопроводности горных пород, показывают, что геотермический градиент, известный для наружных частей земного шара, сохраняется не далее, чем на протяжении первых 20 км ; ниже рост температуры заметно замедляется. У подошвы сиалической оболочки вряд ли температура будет выше 900°; на глубине 100 км — около 1500°; дальше рост ее еще более замедляется. Что касается центральных частей Земли, в частности ядра, то с достоверностью о них оказать что-либо очень трудно. Специалисты, изучавшие этот вопрос, полагают, что недра Земли нагреты не выше, чем на 2–3 тысячи градусов (рис. 11).