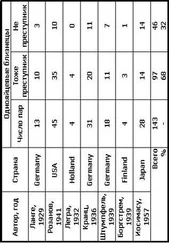
В 1927 году Борсформулировал принципиальное положение квантовой механики – принцип дополнительности,согласно которому получение экспериментальной информации об одних физических величинах, описывающих микрообъект (элементарную частицу, атом, молекулу), неизбежно связано с потерей информации о некоторых других величинах, дополнительных к первым. Такими взаимно дополнительными величинами являются, например, координата частицы и ее импульс (или скорость), потенциальная и кинетическая энергии и др.
Рассмотрим простой пример, который хорошо иллюстрирует принцип дополнительности. Бор обратил внимание на очень простой и понятный факт: координату и импульс микрочастицы нельзя измерить не только одновременно, но и с помощью одного и того же прибора. В самом деле, чтобы измерить импульс микрочастицы и при этом не очень сильно его изменить, необходим очень легкий подвижный прибор. Но именно эта подвижность приводит к тому, что при попадании в такой прибор микрочастицы его положение будет весьма неопределенно. Для измерения координаты мы должны взять другой, очень массивный прибор, который не сдвинется с места при попадании в него микрочастицы. Но в этом случае произойдет изменение импульса микрочастицы, которое прибор даже не заметит. Это простейшая экспериментальная иллюстрация к соотношению неопределенностей Гейзенберга: нельзя в одном и том же опыте определить обе характеристики микрообъекта – координату и импульс. Для этого необходимы два измерения и два принципиально разных прибора, свойства которых дополняют друг друга.
В соответствии с принципом дополнительности волновое и корпускулярное описания микропроцессов не исключают и не заменяют, а дополняют друг друга. Для формирования представления о микрообъекте необходим синтез этих двух описаний.
Квантовый объект – это не частица и не волна, и даже не то и другое одновременно. Квантовый объект – это нечто третье, не равное простой сумме свойств волны и частицы (точно так же, как мелодия – больше, чем сумма составляющих ее звуков). Это квантовое «нечто» не дано нам в ощущение, тем не менее оно, безусловно, реально. У нас нет органов чувств, чтобы вполне представить себе свойства этой реальности. Однако сила нашего интеллекта, опираясь на опыт, позволяет все-таки ее познать.
31. УРАВНЕНИЕ Э. ШРЁДИНГЕРА
Развивая идеи о волновых свойствах материи, австрийский физик-теоретик Э. Шрёдингер(18871961) в 1926 году открыл основное уравнение квантовой механики,описывающее поведение микрочастиц. Оно имеет вид
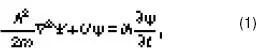
где т – масса частицы;
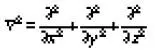
оператор Лапласа, действие которого сводится к получению вторых частных производных функции по координатам; Ψ = Ψ(х, у, z; t) – волновая функция, являющаяся решением уравнения Шрёдингера, которую иногда называют «пси» – функцией; U = U(x, у, z) – потенциальная энергия; 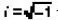 – мнимая единица.
– мнимая единица.
Уравнение Шрёдингера не может быть выведено из других соотношений, оно постулируется. Его справедливость подтверждается тем, что вытекающие из него следствия согласуются с экспериментальными фактами, что придает ему смысл закона природы.
В настоящее время разработан математический аппарат, позволяющий решать уравнение Шрёдингера для различных микрочастиц, например для электронов в атомах, молекулах и в различных веществах. Решить уравнение Шрёдингера – значит найти волновые функции электронов и их энергетический спектр (дозволенные значения энергии). Зная волновые функции, можно рассчитать вероятность нахождения электрона в интересующей области пространства с учетом того, что квадрат модуля волновой функции есть вероятность нахождения электрона в единичном объеме пространства.
В качестве примера рассмотрим поведение электрона в простейшем атоме – атоме водорода. На рис. 1 изображено распределение радиальной плотности вероятности основного состояния электрона (вероятность найти электрон в шаровом слое единичной толщины), полученное из решения уравнения Шрёдингера.
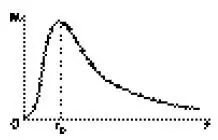
Рис. 1.Распределение радиальной плотности вероятности электрона в основном состоянии в атоме водорода – радиус боровской орбиты)
Читать дальше
Конец ознакомительного отрывка
Купить книгу

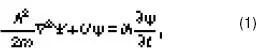
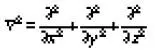
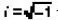 – мнимая единица.
– мнимая единица.