Тим Глинн-Джонс - Странности цифр и чисел.

Отношение диагонали квадрата к его стороне = 1,4142.

Однако V2 известен как иррациональное число, понятие, в которое отказывался верить Пифагор. Иррациональное число — это число, которое не может быть выражено в виде дроби, например х/y, где х и у — целые числа. Один из его учеников, пытаясь выразить V2 в виде дроби, понял, что это невозможно, и ввел понятие «иррациональные числа». По легенде, его утопили за дерзость по указанию Пифагора.

1,618 — «золотое число» фи.

А сейчас вопрос для вас. Что общего у следующих вещей?

Великие египетские пирамиды

Пантеон

Собор Парижской Богоматери

Подсолнух

«Тайная вечеря» Леонардо да Винчи

Скрипка Страдивари

Человеческое тело

Соотношение определенных частей всех этих объектов подчиняется закону «золотого сечения» и равно приблизительно 1,618, оно называется также числом фи (открыто Фибоначчи), «золотым числом» и божественной пропорцией. Чем больше смотришь, тем больше понимаешь его значение. Оно применяется в геометрии, математике, естественных науках и искусстве, оно определяет многие измерения в жизни — в такой, какой мы ее знаем.

Современные исследования «золотого числа» показали, что «золотая пропорция» существует в структуре системы музыкальных звуков и поэтому может применяться для создания превосходной акустики в студиях звукозаписи. Антонио Страдивари, мастер, изготавливающий скрипки в XVII веке, не имел представления об этих исследованиях, но он применял божественную пропорцию в форме своих инструментов и достиг непревзойденного качества звука. Зато Страдивари знал, что в любой музыкальной гамме существуют гармоничные отношения между 1, 3, 5 и 8-м (октава) музыкальными интервалами, которые уже в XII веке связал с «золотым числом» итальянский математик по имени Леонардо Фибоначчи (см. ниже).

Начертите линию. Затем разделите ее на два отрезка так, чтобы соотношение малого отрезка к большому было равно соотношению большого отрезка к целой линии.

Отрезки «золотой пропорции» выражаются иррациональным числом 0,618, а соотношение отрезков, как указано выше, — 1,618. То есть длинный отрезок в 1,618 раза длиннее, чем короткий отрезок, а целая линия в 1,618 раза длиннее, чем длинный отрезок. Греки называли это «обрезать линию в крайнем и среднем соотношении», но это получило более широкую известность под таким поэтичным названием, как «золотое сечение», использование «золотой пропорции». Сходство между соотношением (1,618…) и точкой пропорции линии, где вы поставили отметку, разделяющую отрезки (0,618), не заканчивается тройным многоточием; оно длится до бесконечности.

Вот первое поразительное свойство фи:

1/фи = фи — 1,

то есть 1: 1,618 * 1,618 — 1.

Такое невозможно ни с одним другим числом. Если среди вас есть математики, они выведут из этого еще одно удивительное равенство:

фи 2= фи + 1,

то есть 1,618 х 1,618 * 2,618 = = 1,618 + 1.

Древние египтяне и греки обходились без помощи калькуляторов, которые дают число фи с бесчисленным множеством десятичных разрядов, и применяли его свойства.

Древние математики обнаружили, что «золотое сечение» можно получить при помощи обычной геометрии и, следовательно, применять его в любом масштабе, какой только пожелаешь, даже для строительства великих пирамид.

Вот один из способов, как это можно сделать. Нарисуем равнобедренный треугольник внутри окружности таким образом, чтобы вершины его углов лежали на линии окружности. Проведем от верхнего угла медиану, которая разделит его основание на две равные части. Теперь нарисуем линию, соединяющую середины равных сторон треугольника и пересекающую линию окружности. Точка пересечения медианы и этой линии (центр) будет вершиной прямого угла первичного «золотого треугольника», где катеты (а также отрезки от центра до середины стороны треугольника и до линии окружности) будут иметь отношение, равное фи.

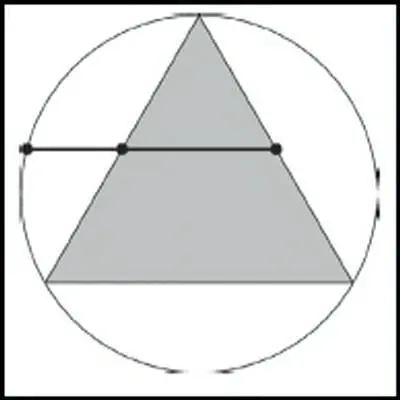
Число фи выражается соотношениями между окружностью и другими правильными геометрическими фигурами, и об этом было известно древним архитекторам, которые искали идеальные пропорции для своих сооружений. Каждый, кто посещал пирамиды в Египте или Пантеон в Афинах, согласится, что они впечатляют.