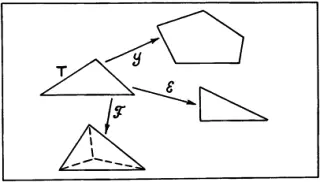
Рис. 24.
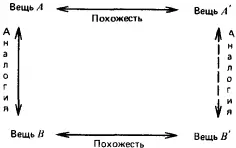
Первая попытка формализовать понятие рассуждения по аналогии была предпринята Лейбницем. В своем сочинении «Фрагменты логики» он ввел понятие пропорции для отношения аналогии. Пропорция Лейбница формулируется следующим образом: «Вещь А так относится к вещи В , как вещь А’ к вещи В’ ». Обычно пропорцию Лейбница представляют в виде диаграммы:
Для иллюстрации того, как может быть использована диаграмма Лейбница, рассмотрим семантическое пространство Осгуда . Это пространство, которое американский психолог Чарльз Осгуд строил экспериментально, проводя опыты с людьми, должно было, по его мнению, характеризовать организацию размещения информации в памяти человека. Мы не будем здесь останавливаться на способе его построения. В комментарии к данному разделу имеется некоторая информация по этому вопросу, а в библиографии заинтересовавшиеся читатели могут найти нужные работы. Скажем только, что упрощенное пространство Осгуда является обычным трехмерным евклидовым пространством. Близость по метрике этого пространства характеризует семантическую близость понятий, фактов и утверждений, а рассуждения, проведенные в пространстве относительно группы элементов, могут проецироваться по аналогии на группы, состоящие из семантически близких элементов.
Проиллюстрируем эту мысль, взяв «кусок» пространства Осгуда, относящийся к понятиям, используемым для указания родства. То, что они в семантическом пространстве расположены компактно, было доказано экспериментально. Этот «кусок» пространства Осгуда показан на рис. 25. Для удобства введена система координат и сделано такое преобразование, чтобы все точки, соответствующие интересующим нас понятиям, оказались лежащими в вершинах единичного куба (правомочность такого преобразования в пространстве Осгуда мы тут не обсуждаем).
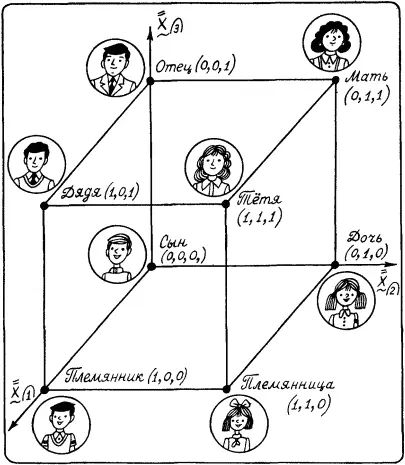
Рис. 25.
Пусть даны три элемента пропорции Лейбница А , А’ и В . И необходимо узнать элемент В’ . Для рассматриваемого примера примем следующий способ нахождения координат понятия В’ : b’ i = b i + а’ i – а i где i =1,2,3. Пусть, например, нас интересует пропорция Сын:Дочь=Дядя:? Для определения неизвестного члена пропорции произведем необходимые вычисления, используя координаты понятий, отмеченные на рис. 25. Получим b’ 1=0+1–0=1; b’ 2=1+0–0=1; b’ 3=0+1–0=1. Таким образом, понятие В’ имеет координаты (1,1,1). Этим координатам соответствует понятие «Тетя».
Для дальнейшего необходимо уточнить понятия «похожесть» и «аналогия», использованные в диаграмме для пропорции Лейбница, и придать им по возможности строгий смысл. Сделать это можно следующим образом. Выберем некоторый алгебраический язык для описания A и В , который обозначим 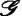 1и некоторый (вообще говоря, другой) алгебраический язык для описания А’ и В’ , который обозначим
1и некоторый (вообще говоря, другой) алгебраический язык для описания А’ и В’ , который обозначим 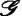 2. Переход от A к В и от A’ к B’ будем интерпретировать как преобразование соответствующих описаний в языках
2. Переход от A к В и от A’ к B’ будем интерпретировать как преобразование соответствующих описаний в языках 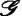 1и
1и 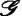 2. Поскольку выбранные языки являются алгебраическими, то в них выделены элементы и операции, определённые над этими элементами. Учитывая дальнейший пример, будем считать, что в качестве элементов языков
2. Поскольку выбранные языки являются алгебраическими, то в них выделены элементы и операции, определённые над этими элементами. Учитывая дальнейший пример, будем считать, что в качестве элементов языков 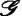 1и
1и 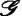 2выступают некоторые изображения или их совокупности, связанные отношениями из заданного набора двуместных отношений. А операции состоят в том, что над элементами можно совершать различные геометрические преобразования, определяемые их движениями. Это приводит к изменению отношений между элементами, входящими в анализируемые совокупности.
2выступают некоторые изображения или их совокупности, связанные отношениями из заданного набора двуместных отношений. А операции состоят в том, что над элементами можно совершать различные геометрические преобразования, определяемые их движениями. Это приводит к изменению отношений между элементами, входящими в анализируемые совокупности.
Чтобы все сказанное стало понятнее, рассмотрим конкретный пример. На рис. 26 показана серия изображений, соответствующая пропорции Лейбница, в которой, как всегда, надо восстановить недостающее звено, т.е. осуществить (если это возможно) вывод по аналогии. Для описания изображений введем языки 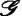 1и
1и 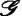 2. В языке
2. В языке 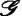 1в качестве элементов возьмем изображение солнца s , и человечка m . В качестве отношений будем рассматривать отношения R 1– «быть слева вверху» и R 2– «быть справа вверху». Тогда ситуация А может быть описана как sR 1 m . В качестве операций в
1в качестве элементов возьмем изображение солнца s , и человечка m . В качестве отношений будем рассматривать отношения R 1– «быть слева вверху» и R 2– «быть справа вверху». Тогда ситуация А может быть описана как sR 1 m . В качестве операций в 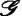 1будем использовать перестановку объектов относительно друг друга O 1и вращение на 180° по часовой стрелке O 2. Тогда преобразование F можно описать как O 1( s , m ); O 2( m ). В результате этого возникает ситуация B , описание которой в языке
1будем использовать перестановку объектов относительно друг друга O 1и вращение на 180° по часовой стрелке O 2. Тогда преобразование F можно описать как O 1( s , m ); O 2( m ). В результате этого возникает ситуация B , описание которой в языке 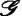 1выглядит как sR 2( O 2( m )).
1выглядит как sR 2( O 2( m )).
Читать дальше




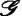 1и некоторый (вообще говоря, другой) алгебраический язык для описания А’ и В’ , который обозначим
1и некоторый (вообще говоря, другой) алгебраический язык для описания А’ и В’ , который обозначим 









