Дмитрий Поспелов - Моделирование рассуждений. Опыт анализа мыслительных актов

О чем все это говорит? Прежде всего о том, что процедура выводимости в исчислении высказываний конструктивно разрешима. Проверка общезначимости (тождественной истинности) формулы сводится к построению нужной конечной таблицы и перебору всех вариантов, содержащихся в ее левой части, с целью определения истинностного значения проверяемой формулы. Получение первого значения «ложь» свидетельствует о невыводимости. Если же при всех комбинациях, перечисленных в левой части таблицы, формула принимает значение «истина», то она выводима с помощью описанных выше двух правил вывода из той или иной полной системы абсолютных аксиом.

Проиллюстрируем эту процедуру еще на одном примере. Проверим, является ли выводимой формула ((? ?) (( ? ?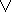)&?)). В этой формуле (будем обозначать ее ?) имеется три высказывания, что приводит к необходимости рассмотрения истинного значения ? на 2 3=8 комбинациях. Эти комбинации и соответствующие шаги по определению истинностного значения ? на них даны в табл. 3, в которой И и Л означают соответственно значения «истина» и «ложь».

Таблица 3

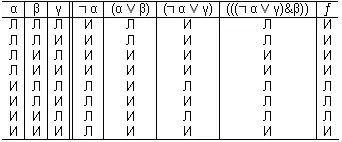
Появление в пятой строке в столбце ? значения Л свидетельствует о невыводимости исследуемой формулы. На этом шаге процесс вывода можно прекратить. Остальные строки в таблице приведены лишь для полноты картины.

Так была названа программа для ЭВМ, созданная в середине шестидесятых годов американским кибернетиком А. Ньюэллом в содружестве с психологом Г. Саймоном. Она была предназначена для доказательства теорем в исчислении высказываний, т.е. для поиска обоснования тождественной истинности некоторых утверждений. Для того чтобы перейти к описанию программы «Логик-теоретик», введем предварительно понятие о равенстве двух выражений исчисления высказываний. Будем говорить, что выражения ? 1и ? 2равны между собой, и записывать этот факт обычным образом ? 1=? 2, если на всех возможных наборах интерпретации истинности входящих в них элементарных высказываний истинность ? 1и ? 2одинакова.

Появление знака равенства, которого не было в исчислении высказываний, не должно нас смущать. Его легко можно исключить из рассмотрения, введя формулу ((? 1&? 2) ( ? 1& ? 2)). Читатели могут проверить, что эта формула будет истинной только в том случае, когда оценки истинности ? 1и ? 2одинаковы. Тогда утверждение, что ? 1=? 2, становится эквивалентным утверждению, что формула ((? 1&? 2) 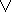( ? 1& ? 2)) является истинной.

«Логик-теоретик» должен был доказывать справедливость утверждений вида ? 1=? 2для различных ? 1и ? 2. Однако авторы «Логика-теоретика» не пошли по прямому пути. Не стали строить таблицы для ? 1и ? 2и проверять совпадение истинности ? 1и ? 2на всех возможных интерпретациях истинности их аргументов. Ведь с ростом числа аргументов n число строк в этих таблицах растет как 2 n . А. Ньюэлл и Г. Саймон пошли по пути приближения процедуры доказательства к тому, как это делают люди.

В основу процесса доказательства они положили идею ликвидации различий в формульной записи ? 1и ? 2. Авторы программы составили перечень из шести различий.

1. В ? 1и ? 2различное число членов в формулах. Например, ? 1=? 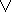?, а ? 2=? 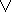? [6].

2. В ? 1и ? 2имеется различие в основной связке (т.е. в связке, которая выполняется последней). Например, ? 1=(??) 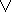( 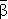), а ? 2=(? ) ?.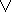

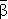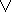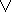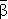3. Перед всем выражением для ? 1(? 2) стоит знак отрицания, а перед ? 2(? 1) его нет. Например, ? 1= (? ?), а ? 2=??.