Проверим, достигаем ли мы нужной цели с помощью данной комбинации. Если ? и ? ложны, то ложны правильные формулы (  ?&?) и (?&
?&?) и (?&  ?) и, следовательно, по свойству дизъюнкции ложна и вся большая формула. Если же ? и ? одновременно истинны, то опять обе конъюнкции ложны, так как в них входят ложные высказывания, получающиеся из истинных путем отрицания, и, следовательно, вся дизъюнкция опять является ложной. И лишь тогда, когда из двух высказываний ? и ? одно истинно, а другое ложно, мы получаем истинность всего высказывания. После этого уточнения правильная формула исчисления высказываний, соответствующая нашему примеру, примет вид (( а &((
?) и, следовательно, по свойству дизъюнкции ложна и вся большая формула. Если же ? и ? одновременно истинны, то опять обе конъюнкции ложны, так как в них входят ложные высказывания, получающиеся из истинных путем отрицания, и, следовательно, вся дизъюнкция опять является ложной. И лишь тогда, когда из двух высказываний ? и ? одно истинно, а другое ложно, мы получаем истинность всего высказывания. После этого уточнения правильная формула исчисления высказываний, соответствующая нашему примеру, примет вид (( а &((  b & c )
b & c ) 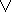 ( b &
( b &  c )))&d).
c )))&d).
Рассмотрим еще одну цитату из того же стихотворения: «…Если трон находится в стране в руках деспо?та, тогда дворянства первая забота сменить основы власти и закон». Введем два элементарных высказывания: g – «Трон находится в стране в руках деспо?та» и h – «Дворянства первая забота сменить основы власти и закон». Тогда логическая структура всего высказывания может быть представлена в виде (ЕСЛИ g ТОГДА h ). Для перехода к правильной формуле исчисления высказываний воспользуемся импликацией. Раньше она не встречалась. По определению выражение ?  ? истинно во всех случаях, кроме того, когда ? истинно, а ? ложно. Другими словами, из истинности ? в импликации, которая является истинной, всегда следует истинность ?.
? истинно во всех случаях, кроме того, когда ? истинно, а ? ложно. Другими словами, из истинности ? в импликации, которая является истинной, всегда следует истинность ?.
Исследуем запись ( g  h ). Если g истинно, то h должно быть истинно, если фраза, которая вложена Д. Самойловым в уста Пестеля, является истинной. Это хорошо, но что будет в случае, когда утверждение g ложно? Для импликации это означает, что как при истинности h , так и при его ложности вся фраза в целом остается истинной. Другими словами, если неверно, что «Трон находится в стране в руках деспо?та», то дворянство может менять основы власти и закона, а может этого и не делать. Всё равно сложное высказывание будет сохранять свою истинность. Если же мы потребуем, чтобы при ложности g всегда было бы ложным и все высказывание целиком, сохраняя остальные свойства импликации, то мы опять вернемся к конъюнкции.
h ). Если g истинно, то h должно быть истинно, если фраза, которая вложена Д. Самойловым в уста Пестеля, является истинной. Это хорошо, но что будет в случае, когда утверждение g ложно? Для импликации это означает, что как при истинности h , так и при его ложности вся фраза в целом остается истинной. Другими словами, если неверно, что «Трон находится в стране в руках деспо?та», то дворянство может менять основы власти и закона, а может этого и не делать. Всё равно сложное высказывание будет сохранять свою истинность. Если же мы потребуем, чтобы при ложности g всегда было бы ложным и все высказывание целиком, сохраняя остальные свойства импликации, то мы опять вернемся к конъюнкции.
Наверное, самым разумным с точки зрения здравого смысла было бы вообще отказаться от определения истинности или ложности выражения (ЕСЛИ ? ТОГДА ?), когда ? является ложным. Ибо для выводов в этом случае нет никакой информации. Во второй главе мы использовали знак выводимости 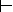 . Вот с его-то помощью и можно формализовать случай, когда в записи g
. Вот с его-то помощью и можно формализовать случай, когда в записи g 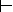 h из истинности g всегда следует истинность h , а при ложности g ничего сказать нельзя. Но знак выводимости не является логической связкой и не входит в синтаксис исчисления высказываний. Поэтому, оставаясь в рамках этого исчисления, мы вынуждены пользоваться импликацией.
h из истинности g всегда следует истинность h , а при ложности g ничего сказать нельзя. Но знак выводимости не является логической связкой и не входит в синтаксис исчисления высказываний. Поэтому, оставаясь в рамках этого исчисления, мы вынуждены пользоваться импликацией.
И еще одно замечание, касающееся импликации. Эта связка, как и разделительная дизъюнкция, может быть сведена к комбинации других связок, имеющихся в исчислении. Читатели легко могут убедиться в справедливости замены ?  ? на
? на  ?
? 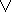 ?. Однако по ряду причин в исчислении высказываний в его классической форме импликация сохраняется как самостоятельная связка [5].
?. Однако по ряду причин в исчислении высказываний в его классической форме импликация сохраняется как самостоятельная связка [5].
Не нужно думать, что переход от фраз на естественном языке к соответствующим им правильным формулам исчисления высказываний столь прост. На этом пути стоит немало трудностей, И прежде всего потому, что частицы и союзы языка типа НЕ, И, ИЛИ, ТО, ЕСЛИ и т.п. не являются однозначными свидетельствами наличия похожих на них связок. Цитата из стихотворения «Смерть поэта» Д. Самойлова иллюстрирует это положение:
И не ведал я, было ли это
Отпеванием времени года,
Воспеваньем страны и народа
Или просто кончиной поэта.
Встречающиеся здесь И и ИЛИ не являются прямыми аналогами связок исчисления высказываний.
Мы ввели множество базовых элементов и множество синтаксических правил. Теперь необходимо ввести множество аксиом. В логике в качестве множества аксиом выбирают обычно совокупность правильных формул, которые являются общезначимыми (или тождественно истинными ). Высказывания, описываемые этими формулами, таковы, что они всегда истинны. Вот пример такого множества формул:
Читать дальше

 ?&?) и (?&
?&?) и (?& 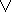 ( b &
( b &  ? истинно во всех случаях, кроме того, когда ? истинно, а ? ложно. Другими словами, из истинности ? в импликации, которая является истинной, всегда следует истинность ?.
? истинно во всех случаях, кроме того, когда ? истинно, а ? ложно. Другими словами, из истинности ? в импликации, которая является истинной, всегда следует истинность ?.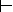 . Вот с его-то помощью и можно формализовать случай, когда в записи g
. Вот с его-то помощью и можно формализовать случай, когда в записи g 









