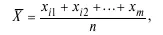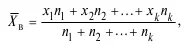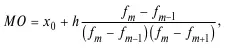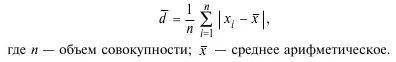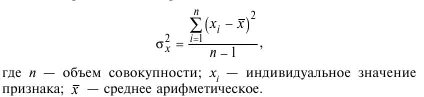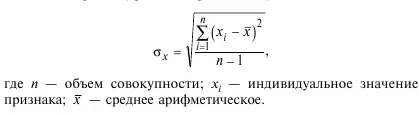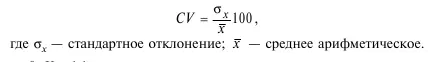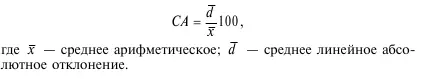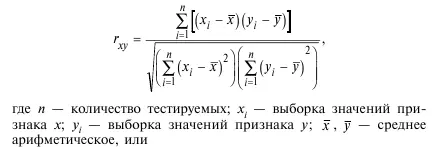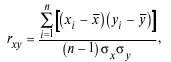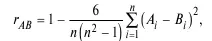Надежда Ефремова - Тестовый контроль в образовании

На практике исследователю необходимо задать себе вопрос, является ли неодинаковое число наблюдений в различных совокупностях в первоначальной выборке отражением истинного распределения или это только (случайный) результат процедуры выбора. В первом случае используются априорные вероятности пропорционально объемам совокупностей в выборке; во втором – априорные вероятности одинаковы для каждой совокупности. Спецификация различных априорных вероятностей может сильно влиять на точность классификации. Для увеличения точности классификаций используются апостериорные вероятности – это вероятности, вычисленные с использованием знания значений других переменных для образцов из частной совокупности. В последнее время созданы программные пакеты, автоматически вычисляющие апостериорные вероятности для различных видов наблюдений. Общим результатом является матрица классификации.

При повторной итерации апостериорная классификация того, что случилось в прошлом, не очень трудна. Нетрудно получить очень хорошую классификацию тех образцов, по которым была оценена функция классификации. Для получения сведений, насколько хорошо работает процедура классификации на самом деле, следует классифицировать (априорно) различные наблюдения, которые не использовались при оценке функции классификации, гибко использовать условия отбора для включения их в число наблюдений или, напротив, исключения. Матрица классификации может быть вычислена по старым образцам столь же успешно, как и по новым. Но только классификация новых наблюдений позволяет определить качество функции классификации, классификация старых наблюдений позволяет лишь провести успешную диагностику наличия выбросов или области, где функция классификации кажется менее адекватной.

Дискриминантный, дисперсионный и факторный анализ являются полезными инструментами для выделения переменных, позволяющих относить наблюдаемые объекты в одну или несколько реально наблюдаемых групп, а также для классификации наблюдений по группам и детального анализа состояния и качества объектов, проведения мониторинговых исследований.

Математический аппарат, используемый для обработки результатов ЕГЭ

(из проекта Типового положения о РЦОИ Псковской области)

1. Среднее арифметическое (простое):

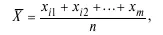
где n – число наблюдений; x i1, x i2, ..., x m – значения переменных.

2. Среднее арифметическое (взвешенное):

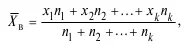
где x i1, x i2, ..., x n – значения переменных; n 1,n 2, ..., n k – веса переменных.

3. Мода:

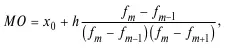
где x 0– нижняя граница модального интервала; h – величина интервала; f m –1– частота интервала, предшествующего модальному; f m + 1– частота интервала, следующего за модальным.

4. Среднее абсолютное (линейное) отклонение:

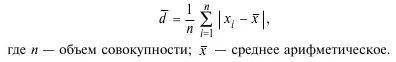
5. Эмпирическая дисперсия:

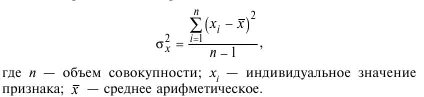
6. Стандартное (среднеквадратическое) отклонение:

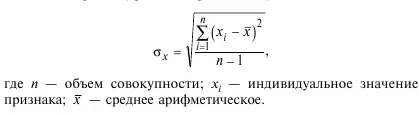
7. Коэффициент вариации Пирсона:

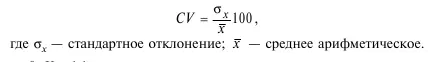
8. Коэффициент ассимиляции:

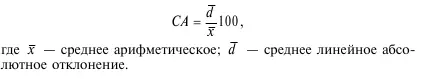
9. Размах (range):

Rx = x max − x min ,

где x max– наибольшее значение наблюдаемого признака; x minнаименьшее значение наблюдаемого признака.

10. Коэффициент корреляции Пирсона:

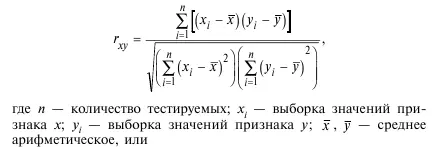
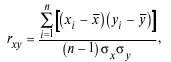
где σ x – стандартное отклонение по х; σ y – стандартное отклонение по у.

11. Коэффициент ранговой корреляции Спирмена:

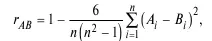
где n – число случаев; A i− B i – разность между индивидуальными рангами по х и у.