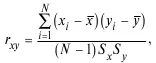Надежда Ефремова: Тестовый контроль в образовании

r сб= 2r xy /(1 + r xy ),

где r сб– коэффициент надежности; rxy – корреляция между двумя половинами шкалы х и у.

Если используемая шкала коррелирует с измеряемым показателем, то можно говорить о достоверности шкалы, т.е. о том, что она действительно измеряет то, для чего создана, а не что–нибудь другое. Построение достоверной выборки – это продолжительный процесс, при котором исследователь изменяет шкалу в соответствии с различными внешними критериями, теоретически связанными с той концепцией, для подтверждения которой и строится шкала. Фактически достоверность шкалы всегда ограничивается ее надежностью, поэтому важной составляющей анализа данных является корреляция, представляющая собой меру взаимозависимости переменных. При заданной надежности двух связанных между собой измерений (т.е. шкалы и исследуемого показателя) можно оценить корреляцию между истинными значениями разных измерений. Это изменение корреляции обусловлено либо значениями, задаваемыми пользователем, либо реальными исходными данными.

Наиболее известна корреляция Пирсона. При вычислении корреляции Пирсона предполагается, что переменные измерены, как минимум, в интервальной шкале. Некоторые другие коэффициенты корреляции могут быть вычислены для менее информативных шкал (порядковых). Коэффициенты корреляции, как правило, изменяются в пределах от–1,00 до +1,00. Значение–1,00 показ ы вает, что переменные имеют строгую отрицательную корреляцию. Значение +1,00 свидетельствует, что переменные имеют строгую положительную корреляцию, а значение 0,00 соответствует отсутствию корреляции.

Наиболее часто используемый коэффициент корреляции Пирсона r называется также линейной корреляцией и измеряет степень линейных связей между переменными. Корреляция Пирсона (далее – корреляция) определяет степень, с которой значения двух переменных пропорциональны друг другу, значение коэффициента корреляции не зависит от масштаба измерения. Например, корреляция между ростом и весом будет одной и той же, независимо от того, проводились измерения в дюймах и фунтах или в сантиметрах и килограммах. Корреляция высокая, если на графике зависимость можно представить прямой линией с положительным или отрицательным углом наклона. Такая прямая называется прямой регрессии, или прямой, построенной методом наименьших квадратов. Последний термин связан с тем, что сумма квадратов расстояний (вычисленных по оси Y) от наблюдаемых точек до прямой является минимальной. Заметим, что использование квадратов расстояний приводит к тому, что оценки параметров прямой сильно реагируют на выбросы.

Коэффициент корреляции Пирсона (r) представляет собой меру линейной зависимости двух переменных x и y :

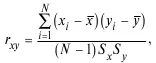
где S x, Sy – стандартные отклонения переменных.

Если возвести его в квадрат, то полученное значение коэффициента детерминации r2 представляет долю вариации, общую для двух переменных, или степень зависимости (связанности этих переменных). Чтобы оценить зависимость между переменными, нужно знать как величину корреляции, так и ее значимость. Уровень значимости, вычисленный для каждой корреляции, зависит от объема выборок и представляет собой главный источник информации о надежности корреляции. Критерий значимости основывается на предположении о том, что распределение отклонений наблюдений от регрессионной прямой для зависимой переменной Y является нормальным с постоянной дисперсией для всех значений независимой переменной X. По определению, выбросы являются нетипичными, резко выделяющимися наблюдениями. Так как при построении прямой регрессии используется сумма квадратов расстояний наблюдаемых точек до прямой, то выбросы могут существенно повлиять на наклон прямой и, следовательно, на значение коэффициента корреляции. Поэтому единичный выброс (значение которого возводится в квадрат) способен существенно изменить наклон прямой и, следовательно, значение корреляции. Если размер выборки относительно мал, то добавление или исключение некоторых данных способно оказать существенное влияние на прямую регресии и коэффициент корреляции. Выбросы могут не только искусственно увеличить значение коэффициента корреляции, но и реально уменьшить существующую корреляцию. Считается, что выбросы представляют собой случайную ошибку, которую следует контролировать. Чтобы не быть введенными в заблуждение полученными значениями, необходимо проверить на диаграмме рассеяния каждый важный случай значимой корреляции.