Шинтан Яу - Теория струн и скрытые измерения Вселенной

В 1989 году, когда связь между моделями Гепнера и многообразиями Калаби-Яу была установлена окончательно, Грин объединился с Плессером в надежде на дальнейшее продвижение. Одним из первых выводов, который им удалось сделать, по словам Грина, стал вывод о том, что «теперь мы имели мощный инструмент для анализа чрезвычайно сложной геометрии [Калаби-Яу] в виде теории поля, которую мы полностью контролируем и полностью понимаем» [96] Ibid. . Их заинтересовал вопрос о том, что произойдет, если они слегка изменят модель Гепнера. Как они полагали, измененная модель будет соответствовать немного отличному многообразию Калаби-Яу. Для начала они применили к модели Гепнера преобразование, отвечающее вращательной симметрии, подобно повороту квадрата на 90 градусов. Эта операция оставила теорию поля неизменной. Однако, выполнив то же преобразование для многообразия Калаби-Яу, они получили многообразие с совершенно иной топологией и совершенно иной геометрией.

Иными словами, преобразование, отвечающее вращательной симметрии, изменило топологию многообразия Калаби-Яу, оставив неизменной сопутствующую ей конформную теорию поля. В результате теперь двум многообразиям Калаби-Яу с совершенно различной топологией можно было сопоставить одну и ту же физическую теорию. «Это, коротко говоря, и называется зеркальной симметрией», — поясняет Гепнер. [97] Doron Gepner, interview with author, August 19, 2008. Используя более общее понятие, можно также определить это свойство как дуальность , смысл которой состоит в том, что два объекта, с виду не имеющие отношения друг к другу, в данном случае — два многообразия Калаби-Яу, тем не менее порождают одну и ту же физику.

Первая статья Грина и Плессера по теме зеркальной симметрии описывала десять так называемых зеркальных партнеров, или зеркальных многообразий, обнаруженных среди нетривиальных и не являющихся совершенно плоскими многообразий Калаби-Яу, начиная с простейшего случая — трехмерной поверхности пятого порядка. Наряду с еще девятью примерами в этой статье содержалась формула, дающая возможность получить зеркальные пары для любой модели Гепнера, — на сегодня число подобных пар составляет сотни, если не тысячи. [98] B. R. Greene and M. R. Plesser, “Duality in Calabi-Yau Moduli Space,” Nuclear Physics В 338 (1990): 15–37.

Зеркальные многообразия имеют ряд интереснейших свойств, проявляющихся при сопоставлении объектов, которые ранее казались не имеющими отношения друг к другу. К примеру, Грин и Плессер обнаружили, что одно из многообразий Калаби-Яу может иметь 101 вариант формы и только один вариант размера; зеркальное же многообразие, напротив, будет иметь 101 вариант размера и единственный вариант формы. Многообразия Калаби-Яу могут иметь дырки различной размерности — как нечетной, так и четной. Грину и Плессеру удалось обнаружить любопытное взаимоотношение между зеркальными парами: число дырок нечетной размерности в многообразии равно числу дырок четной размерности в его зеркальном партнере, и наоборот. «Это означает, что общее число дырок… в обоих многообразиях одинаково, даже несмотря на то, что замена дырок четной размерности на дырки нечетной размерности приводит к совершенно различным формам и геометрическим структурам», — замечает Грин. [99] Brian Greene, The Elegant Universe (New York: Vintage Books, 2000), p. 258.

Рис. 7.1.Брайан Грин (© Андреа Кросса)

Рис. 7.2.Ронен Плессер (Duke Photography)

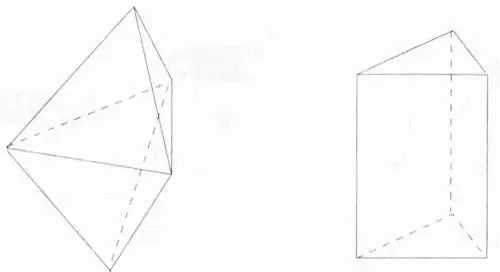
Рис. 7.3.Двойной тетраэдр, имеющий пять вершин и шесть граней, и треугольная призма, имеющая шесть вершин и пять граней, являются простыми примерами зеркальных многообразий. Эти привычные всем многогранники, в свою очередь, можно использовать для создания многообразия Калаби-Яу и его зеркальной пары, причем число вершин и граней многогранника будет определять внутреннюю структуру соответствующего многообразия Калаби-Яу. Подробности процедуры «конструирования» многообразия носят скорее технический характер, выходящий за рамки этого обсуждения

Это еще не объясняет «зеркальный» аспект обнаруженной симметрии, который проще проиллюстрировать при помощи топологии. Было установлено, например, что многообразия Калаби-Яу и их зеркальные партнеры имеют эйлеровы характеристики противоположных знаков, что говорит о существенном различии в их топологиях, хотя и несколько опосредованно, поскольку эти числа сами по себе дают только незначительную часть информации о пространстве и, как уже было показано ранее, многие пространства, заметно отличающиеся друг от друга, такие как куб, тетраэдр и сфера, могут иметь одинаковые эйлеровы характеристики. Можно показать это и более строго, представив эйлеровы характеристики в виде сумм и разностей целых чисел, называемых числами Бетти , которые содержат более полную информацию о внутренней структуре пространства.