Шинтан Яу - Теория струн и скрытые измерения Вселенной

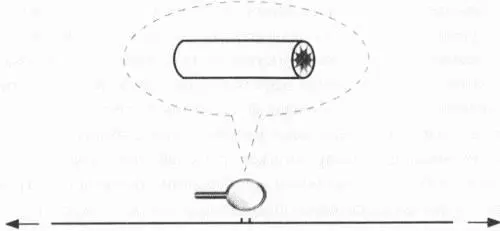
Рис. 1.6.Теория струн взяла на вооружение старую идею Калуцы-Клейна о скрытом «дополнительном» измерении и значительно расширила ее. Если мы внимательно посмотрим на четырехмерное пространство-время, представленное на рисунке в виде линии, то увидим, что на самом деле оно скрывает в себе шесть дополнительных измерений, скрученных в замысловатое, хотя и крошечное геометрическое пространство, известное как многообразие Калаби-Яу. (Более подробно эти пространства будут обсуждаться далее, поскольку они являются основной темой книги.) Какой бы участок линии вы ни вырезали, вы все равно найдете в нем скрытое многообразие Калаби-Яу, и все многообразия, полученные таким способом, будут идентичными

Именно это и пытаются сделать создатели теории струн — захватывающей, хотя и до сих пор не нашедшей экспериментального подтверждения попытки объединить различные взаимодействия путем замены точечных объектов физики элементарных частиц на протяженные (хотя и крошечные) физические объекты, называемые струнами . Как и теория Калуцы-Клейна, теория струн предполагает, что наличие дополнительных измерений помимо тех трех (или четырех), с которыми мы ежедневно сталкиваемся, является необходимым условием для объединения всех сил природы в одну. Большинство вариантов теории струн предполагают существование десяти или одиннадцати (с учетом времени) измерений, необходимых для осуществления Великого объединения.

Но дело не только в том, чтобы ввести несколько дополнительных измерений и надеяться на лучшее. Чтобы теория получила практическое применение, этим измерениям следует поставить в соответствие определенные размеры и формы (вопрос о том, какие именно размеры и формы, — пока остается открытым). Иными словами, геометрия играет в теории струн особую роль, и многие ее сторонники подтвердят, что именно геометрия дополнительных измерений во многом определяет вид той Вселенной, в которой мы живем, обусловливая свойства всех наблюдаемых (а также по тем или иным причинам ненаблюдаемых) в природе физических сил и элементарных частиц.

Начиная с шестой главы мы займемся теорией струн более подробно. Но прежде чем углубиться в сложную математику, лежащую в ее основе, следует более подробно изучить основы геометрии. (Мой, хотя и предвзятый, опыт говорит, что такая методика является удачной.) Поэтому мы отступим на несколько шагов назад от XX и XXI столетий и заглянем в историю этой почтенной науки, чтобы понять, какое место она занимает в существующем порядке вещей.

И если говорить о том месте, которое она занимает, то лично для меня геометрия всегда была чем-то вроде скоростной полосы на автобане истины — наиболее коротким путем из точки, в которой мы находимся, в точку, в которой мы хотим оказаться. Это неудивительно, если принять во внимание, что большая часть геометрических исследований посвящена как раз указанной проблеме — нахождению расстояния между двумя точками. Поэтому запаситесь терпением, если путь от математики Древней Греции к сложнейшим построениям теории струн покажется вам несколько запутанным и извилистым. Порой самый короткий путь — вовсе не самый прямой, в чем мы скоро и убедимся.

Так что же такое геометрия? Многие полагают, что геометрия — это только предмет, который они изучали в средней школе, — совокупность технических приемов, необходимых для измерения углов между прямыми, вычисления площадей треугольников, кругов и прямоугольников и, возможно, для установления некоторой меры эквивалентности между различными геометрическими объектами. Даже если пользоваться столь ограниченным определением, не возникает сомнений, что геометрия является весьма полезным инструментом — к примеру, для архитекторов, ежедневно использующих ее в своей работе. Да, несомненно, геометрия включает в себя все вышеперечисленное, но также и многое другое, поскольку она имеет отношение к архитектуре в самом широком смысле этого слова, начиная от мельчайших масштабов и заканчивая огромнейшими. А для некоторых людей вроде меня, одержимых идеей определения размера, формы, кривизны и структуры космического пространства, геометрия — основной инструмент.