В этом случае p 1, …, p nсуть вероятности элементарных исходов ω 1, …, ω nили просто элементарные вероятности.
Каждому множеству A из ξ(Ω) поставлено в соответствие неотрицательное действительное число P(A). Это число называется вероятностью реализации совокупности исходов. Оно определяется как сумма вероятностей элементарных исходов, входящих в A:
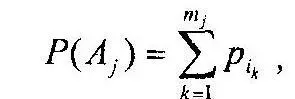
где i k— номера элементарных исходов, входящих в совокупность A j.
Если P(A) > 0, то частное Р(В\А) = Р(АВ)/Р(А), где AB — пересечение множеств А и В, называется условной вероятностью реализации совокупности исходов В при условии реализации совокупности исходов. Отсюда непосредственно следует, что Р(АВ) = Р(В\А)Р(А).
Заключение по индукции даёт общую формулу Р(А 1А 2…А n) = Р(А 1)Р(А 2\А 1)P(A 3\A 2\A 1)…Р(А n\А 1…А n-1) (теорема умножения).
Отсюда получаем Р(А\B) = Р(А)Р(В\А)/Р(B), и далее формулу полной вероятности Р(В) = P(A 1)P(B\A 1) + P(A 2)P(B\A 2) +…+ P(А n)P(B\А n),
где А 1+А 2+…+ А n= Ω и В — произвольная совокупность исходов, и формулу Байеса:
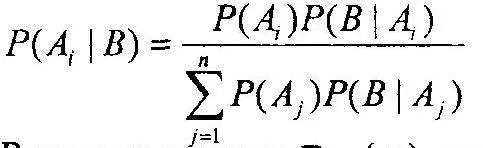
Введение вектора α = {α 1}, где α i=Υр i, позволяет вместо некоторой аддитивной меры, рассматривать метрический вектор единичной длины в евклидовом пространстве. В этом случае вся изложенная выше теория может быть переформулирована в терминах амплитуды вероятности.
Каждому множеству А из ξ(Ω) может быть поставлено в соответствие неотрицательное действительное число Аp(А). Это число называется амплитудой вероятности реализации совокупности исходов А. Оно определяется как корень квадратный из суммы квадратов амплитуд вероятности элементарных исходов, входящих в А:
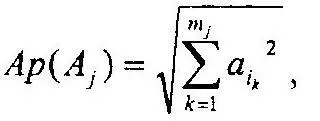
где i k— номера элементарных исходов, входящих в совокупность А j. Ар(Ω) = 1. Если А и B не пересекаются, то [Ap(A+B)] 2=[Ар(А)] 2+ [Ар(В)] 2.
Каждому множеству А j, состоящему из m jэлементарных исходов бифуркационного события, соответствует некоторый m j-мерный евклидов вектор Ар(А j) = {a jk} k = 1,…,m j, модуль которого равняется
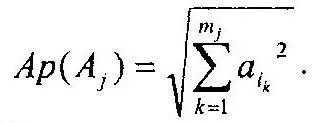
При этом разложение множества А jна сумму взаимно не пересекающихся множеств эквивалентно разложению вектора 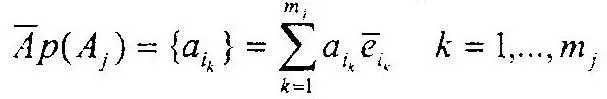
на сумму взаимно ортогональных векторов, каждый из которых имеет координаты, равные амплитудам элементарных событий, входящим в множество, которое он характеризует, е j— орт координаты, характеризующей i-й элементарный возможный исход бифуркационного события.
Формула Байеса переписывается в терминах амплитуды вероятностей следующим образом:
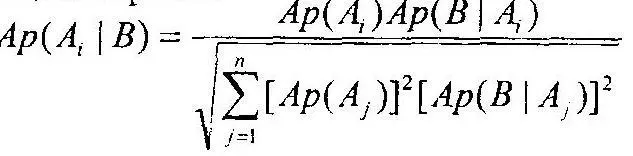
3. Случайные величины и их связь с параметром целого. Комплексный волновой вектор
Пусть дана однозначная функция s(ω) исхода бифуркационного события ω. Тогда функция Р s, определённая формулой Р s(А) = Р{s -1(A)}называется вероятностной функцией s, а функция АР sамплитудой вероятностной функции s.
Функция F s(S) = Р s(-бесконечность, S) = Р {s(ω) < S} называется функцией распределения случайной величины s.
Если свойства состояний системы являются периодическими функциями от s, с периодом h, то назовём величину s действием и вместо величины s введём спиральную переменную, путём отображения прямой линии s на цилиндрическую круговую спираль с основанием цилиндра единичного радиуса.
Точка на этой спирали может быть описана спиральным комплексным числом с единичным модулем e 2ms/h. Проекцией каждого такого числа на комплексную плоскость является точка на окружности единичного радиуса, описываемая алгебраическим комплексным числом e iθ.
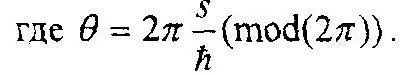
Как величина действия s. так и величина периода действия h, могут быть приняты в качестве параметра целого при исследовании системы на ранних стадиях.
Следующим шагом в анализе бифуркационного события является введение в рассмотрение, по аналогии с действительным вектором вероятности, комплексного волнового вектора Ψ.
Читать дальше

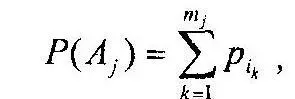
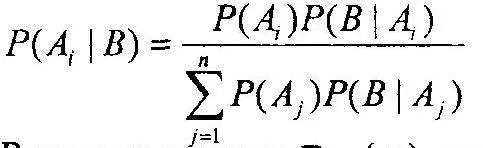
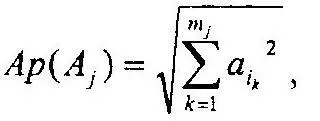
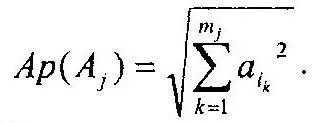
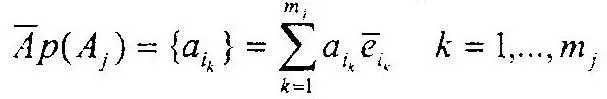
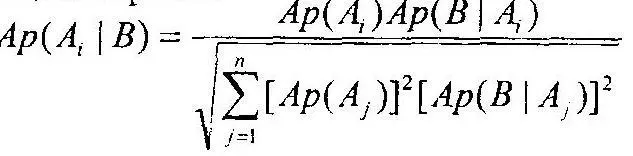
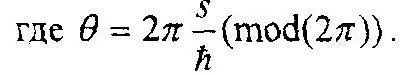






![Марианна Басина - Там, где шумят михайловские рощи [без иллюстраций]](/books/410542/marianna-basina-tam-gde-shumyat-mihajlovskie-rochi-thumb.webp)
![Марианна Басина - Далече от брегов Невы [без иллюстраций]](/books/410545/marianna-basina-daleche-ot-bregov-nevy-bez-illyustr-thumb.webp)

