Аналогичное рассмотрение может быть проведено в общем (абстрактном) случае. Пусть бифуркационное событие имеет два исхода с вероятностями р +, p -,где обе вероятности могут принимать значения в диапазоне 0–1. В результате события вероятность изменяется таким образом, что либо р += 1, либо р += 0.
Так как р ++ p - = 1 , то можно ввести параметр α такой, что р += cos 2α, p - = sin 2α.
Отсюда следует, что величину α можно представить себе в виде единичного вектора α = {α x, α y}где α х= cosα, α y = sinα. Квадраты проекций вектора α на оси х, у равны соответствующим вероятностям α 2 x= р +, α 2 y= Р -
Таким образом, выбор того или иного результата события может быть связан с вращением вектора α в двумерном пространстве.
Пусть количество вариантов результатов данного события равно n. В результате события реализуется лишь одна из возможностей. Перед событием существует вероятность реализации каждой из возможностей p r. Сумма вероятностей реализации каждого из указанных исходов равна единице:
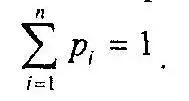
В результате свершения события вероятность реализации одного из результатов окажется равной 1, а вероятность того, что наступит какой-либо другой исход, окажется равной нулю. Набор вероятностей p — вероятностный вектор — коллапсирует к одному из единичных векторов, то есть он коллапсирует к одному из ортов системы координат, сформированных возможными исходами события.
Итак, перед самым событием существует некоторый вектор р, характеризующий распределение возможностей реализации тех или иных возможных результатов события. Этот вектор может быть назван вектором вероятности будущего события, n-мерный вектор p перед событием может, в принципе, принимать любые значения на n-1 — мерном многообразии, имеющем уравнение:
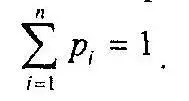
Предыдущий опыт может приближенно подсказать точку на многообразии, соответствующую моменту, предшествующему изучаемому нами событию, однако мы не можем предсказать точно, что произойдет в результате события.
Совсем по иному выглядит картина после происшедшего события. Событие произошло. Определенный результат реализовался, остальные не реализовались. Вектор p принял одно из n возможных значений. Можно сказать, что событие подействовало как оператор, резко уменьшивший область допустимых значений вектора p — c n— 1 — мерного многообразия — до одной из точек.
То же самое можно сформулировать и по-другому. Соотношения вероятностей попадания системы в одно из возможных состояний до и после события резко изменились. До события система еще имела возможность попасть в любое из допустимых состояний. После события возможность попадания во все состояния, кроме одного, оказались равными нулю.
Наблюдатель системы приобрёл значительную новую информацию не только о настоящем, но и о будущем системы. Здесь, как и ранее для случая с двумя исходами интуитивно появляется понятие информации как результата отождествления системы, которая до свершения события могла с некоторой вероятностью оказаться в одном из возможных состояний с некоторым конкретным состоянием.
Нашему рассмотрению может быть дана и другая математическая интерпретация. Пусть мы имеем фазовое пространство взаимодействующих структур, имеющее n аттракторов — зон притяжения; существует некоторая точка (или область), отделяющая друг от друга бассейны притяжения этих аттракторов. Перед событием фазовое состояние системы взаимодействующих структур попадает в указанную точку или область, выйдя из которой в процессе события оно попадает в бассейн притяжения того или иного аттрактора, откуда ей уже не вернуться назад.
В классической теории вероятностей вместо вектора/) вводится некоторая функция на множестве возможных исходов бифуркационного (случайного) события.
Рассматривается в элементарном случае конечное множество Ω элементов ω, которые мы будем называть элементарными исходами бифуркационного события и ξ(Ω) множество подмножеств из Ω. Элементы множества φ(Ω) будем называть совокупностями исходов бифуркационного события, а Ω — пространством элементарных исходов бифуркационного события.
Каждому элементу ω из Ω поставлено в соответствие неотрицательное действительное число p 1, — вероятность реализации i-го исхода бифуркационного события. При этом выполняется условие 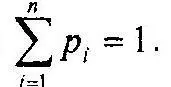
Читать дальше

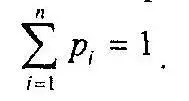
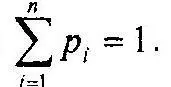






![Марианна Басина - Там, где шумят михайловские рощи [без иллюстраций]](/books/410542/marianna-basina-tam-gde-shumyat-mihajlovskie-rochi-thumb.webp)
![Марианна Басина - Далече от брегов Невы [без иллюстраций]](/books/410545/marianna-basina-daleche-ot-bregov-nevy-bez-illyustr-thumb.webp)

