Нассим Талеб - The Black Swan. The Impact of the Highly Improbable

The strangest thing is that people in business usually agree with me when they listen to me talk or hear me make my case. But when they go to the office the next day they revert to the Gaussian tools so entrenched in their habits. Their minds are domain-dependent, so they can exercise critical thinking at a conference while not doing so in the office. Furthermore, the Gaussian tools give them numbers, which seem to be “better than nothing.” The resulting measure of future uncertainty satisfies our ingrained desire to simplify even if that means squeezing into one single number matters that are too rich to be described that way.

The Clerks’ Betrayal

I ended Chapter 1 with the stock market crash of 1987, which allowed me to aggressively pursue my Black Swan idea. Right after the crash, when I stated that those using sigmas (i.e., standard deviations) as a measure of the degree of risk and randomness were charlatans, everyone agreed with me. If the world of finance were Gaussian, an episode such as the crash (more than twenty standard deviations) would take place every several billion lifetimes of the universe (look at the height example in Chapter 15). According to the circumstances of 1987, people accepted that rare events take place and are the main source of uncertainty. They were just unwilling to give up on the Gaussian as a central measurement tool—“Hey, we have nothing else.” People want a number to anchor on. Yet the two methods are logically incompatible.

FIGURE 14

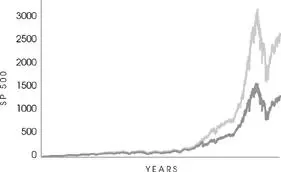
By removing the ten biggest one-day moves from the U.S. stock market over the past fifty years, we see a huge difference in returns—and yet conventional finance sees these one-day jumps as mere anomalies. (This is only one of many such tests. While it is quite convincing on a casual read, there are many more-convincing ones from a mathematical standpoint, such as the incidence of 10 sigma events.)

Unbeknownst to me, 1987 was not the first time the idea of the Gaussian was shown to be lunacy. Mandelbrot proposed the scalable to the economics establishment around 1960, and showed them how the Gaussian curve did not fit prices then . But after they got over their excitement, they realized that they would have to relearn their trade. One of the influential economists of the day, the late Paul Cootner, wrote, “Mandelbrot, like Prime Minister Churchill before him, promised us not utopia, but blood, sweat, toil, and tears. If he is right, almost all our statistical tools are obsolete [or] meaningless.” I propose two corrections to Cootner’s statement. First, I would replace almost all with all . Second, I disagree with the blood and sweat business. I find Mandelbrot’s randomness considerably easier to understand than the conventional statistics. If you come fresh to the business, do not rely on the old theoretical tools, and do not have a high expectation of certainty.

Anyone Can Become President

And now a brief history of the “Nobel” Prize in economics, which was established by the Bank of Sweden in honor of Alfred Nobel, who may be, according to his family who wants the prize abolished, now rolling in his grave with disgust. An activist family member calls the prize a public relations coup by economists aiming to put their field on a higher footing than it deserves. True, the prize has gone to some valuable thinkers, such as the empirical psychologist Daniel Kahneman and the thinking economist Friedrich Hayek. But the committee has gotten into the habit of handing out Nobel Prizes to those who “bring rigor” to the process with pseudoscience and phony mathematics. After the stock market crash, they rewarded two theoreticians, Harry Markowitz and William Sharpe, who built beautifully Platonic models on a Gaussian base, contributing to what is called Modern Portfolio Theory. Simply, if you remove their Gaussian assumptions and treat prices as scalable, you are left with hot air. The Nobel Committee could have tested the Sharpe and Markowitz models—they work like quack remedies sold on the Internet—but nobody in Stockholm seems to have thought of it. Nor did the committee come to us practitioners to ask us our opinions; instead it relied on an academic vetting process that, in some disciplines, can be corrupt all the way to the marrow. After that award I made a prediction: “In a world in which these two get the Nobel, anything can happen. Anyone can become president.”

So the Bank of Sweden and the Nobel Academy are largely responsible for giving credence to the use of the Gaussian Modern Portfolio Theory as institutions have found it a great cover-your-behind approach. Software vendors have sold “Nobel crowned” methods for millions of dollars. How could you go wrong using it? Oddly enough, everyone in the business world initially knew that the idea was a fraud, but people get used to such methods. Alan Greenspan, the chairman of the Federal Reserve bank, supposedly blurted out, “I’d rather have the opinion of a trader than a mathematician.” Meanwhile, the Modern Portfolio Theory started spreading. I will repeat the following until I am hoarse: it is contagion that determines the fate of a theory in social science, not its validity.

I only realized later that Gaussian-trained finance professors were taking over business schools, and therefore MBA programs, and producing close to a hundred thousand students a year in the United States alone, all brainwashed by a phony portfolio theory. No empirical observation could halt the epidemic. It seemed better to teach students a theory based on the Gaussian than to teach them no theory at all. It looked more “scientific” than giving them what Robert C. Merton (the son of the sociologist Robert K. Merton we discussed earlier) called the “anecdote.” Merton wrote that before portfolio theory, finance was “a collection of anecdotes, rules of thumb, and manipulation of accounting data.” Portfolio theory allowed “the subsequent evolution from this conceptual potpourri to a rigorous economic theory.” For a sense of the degree of intellectual seriousness involved, and to compare neoclassical economics to a more honest science, consider this statement from the nineteenth-century father of modern medicine, Claude Bernard: “Facts for now, but with scientific aspirations for later.” You should send economists to medical school.

So the Gaussian *pervaded our business and scientific cultures, and terms such as sigma, variance, standard deviation, correlation, R square , and the eponymous Sharpe ratio , all directly linked to it, pervaded the lingo. If you read a mutual fund prospectus, or a description of a hedge fund’s exposure, odds are that it will supply you, among other information, with some quantitative summary claiming to measure “risk.” That measure will be based on one of the above buzzwords derived from the bell curve and its kin. Today, for instance, pension funds’ investment policy and choice of funds are vetted by “consultants” who rely on portfolio theory. If there is a problem, they can claim that they relied on standard scientific method.

More Horror

Things got a lot worse in 1997. The Swedish academy gave another round of Gaussian-based Nobel Prizes to Myron Scholes and Robert C. Merton, who had improved on an old mathematical formula and made it compatible with the existing grand Gaussian general financial equilibrium theories—hence acceptable to the economics establishment. The formula was now “useable.” It had a list of long forgotten “precursors,” among whom was the mathematician and gambler Ed Thorp, who had authored the bestselling Beat the Dealer , about how to get ahead in blackjack, but somehow people believe that Scholes and Merton invented it, when in fact they just made it acceptable. The formula was my bread and butter. Traders, bottom-up people, know its wrinkles better than academics by dint of spending their nights worrying about their risks, except that few of them could express their ideas in technical terms, so I felt I was representing them. Scholes and Merton made the formula dependent on the Gaussian, but their “precursors” subjected it to no such restriction. *