Нассим Талеб - The Black Swan. The Impact of the Highly Improbable

Again, Poincaré is in a class by himself. I recall my father recommending Poincaré’s essays, not just for their scientific content, but for the quality of his French prose. The grand master wrote these wonders as serialized articles and composed them like extemporaneous speeches. As in every masterpiece, you see a mixture of repetitions, digressions, everything a “me too” editor with a prepackaged mind would condemn—but these make his text even more readable owing to an iron consistency of thought.

Poincaré became a prolific essayist in his thirties. He seemed in a hurry and died prematurely, at fifty-eight; he was in such a rush that he did not bother correcting typos and grammatical errors in his text, even after spotting them, since he found doing so a gross misuse of his time. They no longer make geniuses like that—or they no longer let them write in their own way.

Poincaré’s reputation as a thinker waned rapidly after his death. His idea that concerns us took almost a century to resurface, but in another form. It was indeed a great mistake that I did not carefully read his essays as a child, for in his magisterial La science et l’hypothèse , I discovered later, he angrily disparages the use of the bell curve.

I will repeat that Poincaré was the true kind of philosopher of science: his philosophizing came from his witnessing the limits of the subject itself, which is what true philosophy is all about. I love to tick off French literary intellectuals by naming Poincaré as my favorite French philosopher. “Him a philosophe? What do you mean, monsieur?” It is always frustrating to explain to people that the thinkers they put on the pedestals, such as Henri Bergson or Jean-Paul Sartre, are largely the result of fashion production and can’t come close to Poincaré in terms of sheer influence that will continue for centuries to come. In fact, there is a scandal of prediction going on here, since it is the French Ministry of National Education that decides who is a philosopher and which philosophers need to be studied.

I am looking at Poincaré’s picture. He was a bearded, portly and imposing, well-educated patrician gentleman of the French Third Republic, a man who lived and breathed general science, looked deep into his subject, and had an astonishing breadth of knowledge. He was part of the class of mandarins that gained respectability in the late nineteenth century: upper middle class, powerful, but not exceedingly rich. His father was a doctor and professor of medicine, his uncle was a prominent scientist and administrator, and his cousin Raymond became a president of the republic of France. These were the days when the grandchildren of businessmen and wealthy landowners headed for the intellectual professions.

However, I can hardly imagine him on a T-shirt, or sticking out his tongue like in that famous picture of Einstein. There is something non-playful about him, a Third Republic style of dignity.

In his day, Poincaré was thought to be the king of mathematics and science, except of course by a few narrow-minded mathematicians like Charles Hermite who considered him too intuitive, too intellectual, or too “hand-waving.” When mathematicians say “hand-waving,” disparagingly, about someone’s work, it means that the person has: a) insight, b) realism, c) something to say, and it means that d) he is right because that’s what critics say when they can’t find anything more negative. A nod from Poincaré made or broke a career. Many claim that Poincaré figured out relativity before Einstein—and that Einstein got the idea from him—but that he did not make a big deal out of it. These claims are naturally made by the French, but there seems to be some validation from Einstein’s friend and biographer Abraham Pais. Poincaré was too aristocratic in both background and demeanor to complain about the ownership of a result.

Poincaré is central to this chapter because he lived in an age when we had made extremely rapid intellectual progress in the fields of prediction—think of celestial mechanics. The scientific revolution made us feel that we were in possession of tools that would allow us to grasp the future. Uncertainty was gone. The universe was like a clock and, by studying the movements of the pieces, we could project into the future. It was only a matter of writing down the right models and having the engineers do the calculations. The future was a mere extension of our technological certainties.

The Three Body Problem

Poincaré was the first known big-gun mathematician to understand and explain that there are fundamental limits to our equations. He introduced nonlinearities, small effects that can lead to severe consequences, an idea that later became popular, perhaps a bit too popular, as chaos theory. What’s so poisonous about this popularity? Because Poincaré’s entire point is about the limits that nonlinearities put on forecasting; they are not an invitation to use mathematical techniques to make extended forecasts. Mathematics can show us its own limits rather clearly.

There is (as usual) an element of the unexpected in this story. Poincaré initially responded to a competition organized by the mathematician Gösta Mittag-Leffer to celebrate the sixtieth birthday of King Oscar of Sweden. Poincaré’s memoir, which was about the stability of the solar system, won the prize that was then the highest scientific honor (as these were the happy days before the Nobel Prize). A problem arose, however, when a mathematical editor checking the memoir before publication realized that there was a calculation error, and that, after consideration, it led to the opposite conclusion—unpredictability, or, more technically, nonintegrability. The memoir was discreetly pulled and reissued about a year later.

Poincaré’s reasoning was simple: as you project into the future you may need an increasing amount of precision about the dynamics of the process that you are modeling, since your error rate grows very rapidly. The problem is that near precision is not possible since the degradation of your forecast compounds abruptly—you would eventually need to figure out the past with infinite precision. Poincaré showed this in a very simple case, famously known as the “three body problem.” If you have only two planets in a solar-style system, with nothing else affecting their course, then you may be able to indefinitely predict the behavior of these planets, no sweat. But add a third body, say a comet, ever so small, between the planets. Initially the third body will cause no drift, no impact; later, with time, its effects on the two other bodies may become explosive. Small differences in where this tiny body is located will eventually dictate the future of the behemoth planets.

FIGURE 2: PRECISION AND FORECASTING

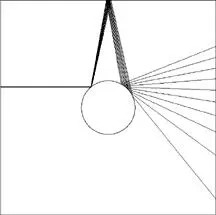
One of the readers of a draft of this book, David Cowan, gracefully drew this picture of scattering, which shows how, at the second bounce, variations in the initial conditions can lead to extremely divergent results. As the initial imprecision in the angle is multiplied, every additional bounce will be further magnified. This causes a severe multiplicative effect where the error grows out disproportionately.

Explosive forecasting difficulty comes from complicating the mechanics, ever so slightly. Our world, unfortunately, is far more complicated than the three body problem; it contains far more than three objects. We are dealing with what is now called a dynamical system—and the world, we will see, is a little too much of a dynamical system.