Андрей Павлов - Геометрия - Планиметрия в тезисах и решениях. 9 класс

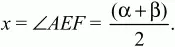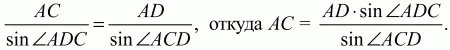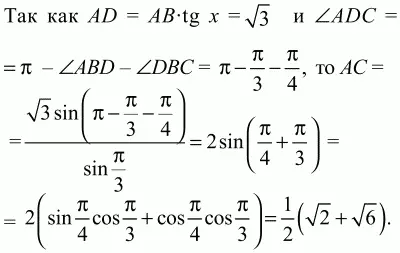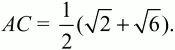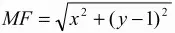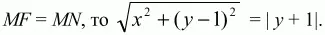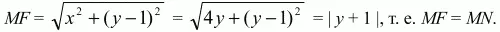
Рис. 293.

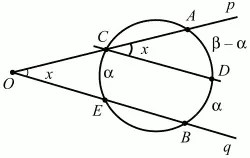
Решение I (рис. 293). Обозначим точки пересечения окружности лучами р и q соответственно через С, А и Е, В. Проведём CD||ЕВ. Получим угол ?ACD = х. Угол ?ACD является вписанным в окружность и по определению равен половине дуги AD. По условию задачи дуга СЕ = ?, а дуга АВ равна ?. Тогда дуга AD = ? – ?. В таком случае х = 1/2 (? – ?).

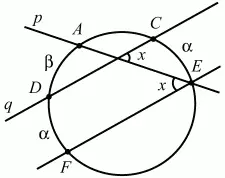
Рис. 294.

Решение II (рис. 294). Обозначим точки пересечения окружности прямыми р и q соответственно через А, Е и D, С. Проведём EF||CD. Угол AEF будет равен х (как внутренние накрест лежащие углы при параллельных CD, FE и секушей АЕ). ?AEF является вписанным в окружность и равен половине дуги AF. Из условия задачи и построений следует, что дуга AF = ? + ?.

Следовательно,

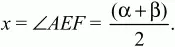
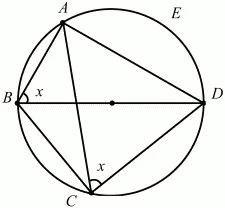
Рис. 295.

Решение. Так как BD – диаметр окружности, то ?BAD = ?BCD = ?/2. Обозначим ?ABD через х, тогда из прямоугольного треугольника ABD получаем, что cos х = AB/BD. По условию BD = 2, АВ = 1, значит, cos х = 1/2, и так как х – внутренний угол прямоугольного треугольника ABD, то х = ?/3. Тогда ?DBC = 3/4 (?ABD) = 3/4 ? ?/3 = ?/4. Вписанные углы ACD и ABD опираются на одну и ту же дугу AED, значит, ?ACD = ?ABD = ?/3. Из треугольника ADC по теореме синусов получаем, что

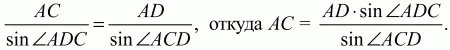
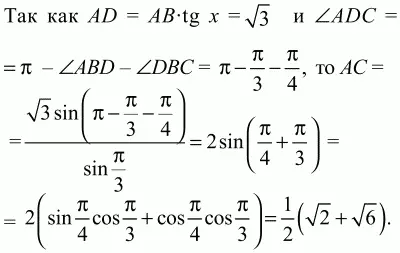
Ответ:

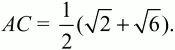
Решение. OB = 4; ВС = 3, значит ОС = 7. OB ? ОС = ОА2; 4 ? 7 = OA2; OA = 2?7.

Ответ: 2?7.

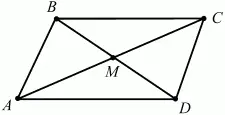
Рис. 296.

Решение. Достроим ?ABD до параллелограмма. Тогда АС < АВ + ВС, но АС = 2AM, 2AM < АВ + ВС = АВ + AD, что и требовалось доказать. Заметим, что AM является медианой ?ABD.

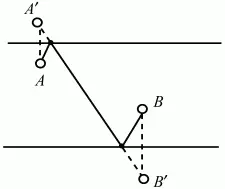
Рис. 297.

Решение. Достаточно построить симметричные точки относительно берегов и длина полученной ломаной равна длине прямолинейного отрезка А'В', т. е. минимальна.

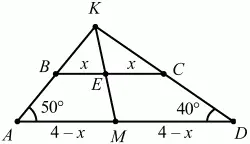
Рис. 298.

Решение. Так как средняя линия трапеции ABCD равна 4, то сумма оснований равна 8. Воспользуемся тем, что середины оснований и точка пересечения боковых сторон трапеции лежат на одной прямой КМ. Из ?AKD ?AKD = 90°. Заметим, что ?AKD – прямоугольный, причем AD – гипотенуза и точкой М делится пополам. Но тогда AM = MD = КМ = 4 – х (радиусы описанной около ?AKD окружности), КЕ = 3 – х, где х – это длина отрезков BE и ЕС. Из подобия ?АКМ и ?ВКЕ следует: (4 – х)/x = (4 – х)/(3 – x); x = 3/2; BC = 3, AD = 5.

Ответ: 5 и 3.

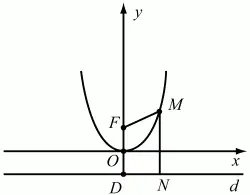
Рис. 299.

Решение. Пусть D – проекция точки F на прямую d. Середину О отрезка DF примем за начало прямоугольной системы координат, а прямую OF – за ось ординат. Точке F отнесём координаты (0; 1). Прямая d будет иметь уравнение у = -1. Пусть М(х; y) – произвольная точка плоскости. Тогда

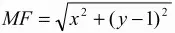
и MN = |у + 1 |, где MN – расстояние от точки М до прямой d. Если

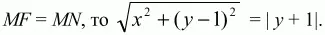
Возведя обе части в квадрат, получим уравнение у = 1/4x2.

Обратно, если координаты точки М удовлетворяют этому уравнению, то х2= 4у и, следовательно,

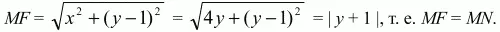
Заметим, что если вместо DF = 2 положить DF = р, то получим уравнение х2= 2ру.

Из школьного курса алгебры известно, что линия, определяемая уравнением у = ах2, называется параболой.