Жуан Гомес - Мир математики. т.4. Когда прямые искривляются. Неевклидовы геометрии

«Прямая, параллельная данной прямой, сохраняет постоянное расстояние от нее».

* * *

ГЕОМЕТРИЯ В ИСКУССТВЕ

Художники в своих работах используют точки, прямые линии и другие геометрические объекты. Их работы очень помогают при ответе на вопросы «что такое точка?», «что такое прямая линия?», «что мы имеем в виду под параллельностью?» Василий Кандинский(1866–1944) был русским художником, поэтом, драматургом и педагогом. Научные исследования в области права и экономики он сочетал с занятиями графикой и живописью. Его преподавательский опыт отражен в трактате «Точка и линия на плоскости» (1925), где Кандинский определил прямую линию как «след перемещающейся точки».

* * *

Великий французский математик Адриен Мари Лежандр(1752–1833) пытался доказать пятый постулат в книге «Начала геометрии», которая многократно переиздавалась и переводилась на многие языки. Более 40 лет он искал доказательство пятого постулата, которое было бы математически строгим, но в то же время понятным читателям и студентам. К сожалению, он умер, так и не увидев развития неевклидовых геометрий. Однако именно он сформулировал постулат для углов треугольника:

«Существует треугольник, сумма углов которого равна двум прямым».

Тут мы должны упомянуть Яноша Бойяи, о котором мы позже расскажем более подробно. Отец Бойяи, который также был математиком, безуспешно пытался доказать пятый постулат и поэтому не хотел, чтобы его сын зря тратил время на решение этой задачи. Однако Яношу было суждено сделать гораздо большее. Все началось с постулата о трех точках:

«Через любые три точки, не лежащие на прямой линии, всегда можно провести окружность».

Мы также более подробно рассмотрим результаты «принца математики» Карла Фридриха Гаусса, который начал работать над пятым постулатом в 1792 г. в возрасте 15 лет и к 1817 г. убедился, что этот постулат совершенно независим от других четырех. Гаусс сформулировал постулат о площади треугольника:

«Существует треугольник сколь угодно большой площади».

Особенно важным был результат шотландского математика и геолога Джона Плейфера(1748–1819). Именно его «аксиома параллельности», в отличие от сложной формулировки Евклида, в настоящее время преподается в школах и наиболее часто встречается в учебниках. И действительно, ее часто принимают за оригинальную формулировку пятого постулата Евклида. Ее ценность заключается в простоте — аксиому Плейфера гораздо легче понять, чем формулировку Евклида:

«В плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной».

Эту аксиому также можно сформулировать следующим образом: через точку, не лежащую на данной прямой, можно провести только одну прямую, которая не пересекает данную прямую (см. рис. V' на стр. 31).

Как бы то ни было, даже такое ясное и очевидное утверждение, как аксиома Плейфера не смогло убедить многих геометров. Откуда же эта одержимость идеей бросить вызов бессмертному Евклиду?

* * *

ТЕОРЕМА О БОЛЬШОЙ ТОЧКЕ

Эта теорема представляет собой довольно необычный результат, который можно сформулировать следующим образом:

«Число прямых, параллельных данной прямой, которые можно провести через точку вне этой прямой, зависит от того, насколько большой является эта точка».

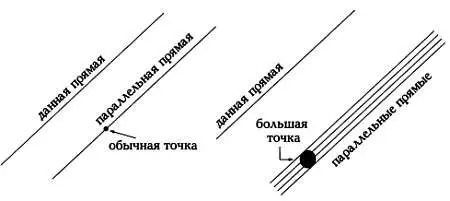
Через большую точку вне прямой можно провести более одной прямой, параллельной данной.

Из этого также следует, что «через большую точку вне прямой можно провести сколь угодно много параллельных (и перпендикулярных) прямых к данной прямой».

Конечно, это всего лишь математическая шутка, но тем не менее эта формулировка наводит на интересные мысли. Откуда мы знаем, сколько линий (в евклидовом смысле) содержится в кончике грифеля карандаша? Чтобы проверить параллельность этих линий, нам придется продолжить их в бесконечность, а на это не хватит никакой бумаги в мире. Поэтому пятый постулат Евклида не может быть доказан экспериментально.

* * *

Эта одержимость объединяла Леонардо да Винчи (1452–1519) и Альбрехта Дюрера(1471–1528) , превратив их в выдающихся художников эпохи Возрождения и в величайших теоретиков за всю историю искусства. В своем трактате Institutiones Geometricae (латинский перевод с немецкого Underweysung der Messung , «Об измерениях»), опубликованном в Германии в 1525 г., Дюрер писал: