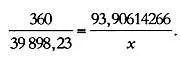Жуан Гомес - Мир математики. т.4. Когда прямые искривляются. Неевклидовы геометрии

cos d = cos a · cos b + sin a · sin b · cos D .

Чтобы найти d , мы должны знать величины сторон а и b и угла D . Чтобы вычислить длину стороны сферического треугольника, возьмем экватор за горизонтальную ось и вычтем из 90° широту каждой точки. Для нахождения угла D мы поступаем аналогично, на этот раз беря в качестве оси координат Гринвичский меридиан:

а = 90°- 41° = 49°

Ь = 90–36° = 34°

D = 140°- 2° = 138°.

Подставляя эти значения в теорему косинусов и используя калькулятор, получим:

cos (d) = cos(49°)·cos(54°) + sin(49°)·sin(54°)·cos(138°) =

= 0,656059029·0,5877852523 + 0,7547095802·0,809016944·(-0,7431448255) =

= -0,06812225162.

Используя клавишу cos -1, мы найдем расстояние d: 93,90614266°.

Однако, было бы более полезно определить это расстояние в километрах. Учитывая, что радиус Земли составляет 6350 км, длина окружности большого круга на поверхности земного шара может быть вычислена по формуле:

2·π·R = 2·π·6350 = 39 898,23 км.

Таким образом, длина 39898,23 км соответствует полному кругу в 360°. Остается узнать, скольким километрам соответствует угол в 93,90614266°.

Обозначим это значение за х и посчитаем следующую пропорцию:

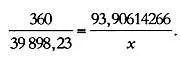
Выражая отсюда х , получим х = 10407,46911 км.

Первая страница приложения Google™ Планета Земляпозволяет «перенестись» в любую точку планеты и рассчитать расстояние между двумя точками на поверхности Земли.

Таким образом, расстояние между Токио и Барселоной составляет около 10407 км. Пожалуй, самое удивительное, что этот результат может быть получен лишь с помощью координат на карте мира.

Современные технологии позволяют рассчитывать расстояния с гораздо большей точностью. Такие программы, как Google™ Планета Земля, позволяют сделать эти расчеты очень быстро и точно. Например, Google™ Планета Земля показывает, что расстояние от Барселоны до Токио равно 10442,62 км.

Расчеты, сделанные вручную, как, например, приведенные выше, не слишком отличаются от результатов специализированного программного обеспечения. Результат программы Google™ Планета Земля отличается от нашего лишь на 35 км. Однако эти компьютерные программы позволяют вычислять расстояния между конкретными точками, например, между конкретными зданиями на той или иной улице.

Такие сложные расчеты невозможно сделать с помощью обычной бумажной карты мира. На самом деле использование компьютеров породило новую область геометрии под названием вычислительная геометрия .

Наш рассказ о геометрии поверхности Земли мы закончим классическим описанием сферы из диалога Платона «Тимей, или О природе»:

«По такой причине Бог построил во всем его разнообразии единое целое, совершенное и непричастное дряхлению и недугам. Что касается формы целого, то ему подобают такие очертания, которые содержат в себе все другие. Именно поэтому Он округлил Землю до состояния сферы, поверхностъ которой повсюду равно отстоит от центра. Эти очертания из всех очертаний наиболее совершенные и подобные самим себе, потому что подобное он нашел в мириады раз более прекрасным, чем неподобное».

Открытие неевклидовых пространств совершенно изменило роль геометрии. Древняя наука об «измерении форм» проникла во все области человеческого знания. Геометрия превратилась из математического ручейка в полноводное море, она перестала быть ограничена узкими рамками евклидова мира и теперь сама открывает безграничный простор воображению. Из наблюдения за объектами и явлениями возникли различные другие виды геометрии. Именно геометрия повышает сложность науки.

В этой главе мы подробнее — хотя, конечно, не во всей полноте — рассмотрим возрастающую важность геометрии в наше время.

В конце XX века появился раздел геометрии, который включил в себя статистику и теорию вероятностей. Эта современная геометрия, совершенно не похожая на евклидову, называется интегральной геометрией. Одним из ее основоположников был Луи Сантало (1911–2001), выдающийся испанский математик и педагог. Как это часто бывает, новая дисциплина возникла при попытке решить классическую задачу. Результаты многолетних исследований Сантало опубликовал в своей книге «Интегральная геометрия и геометрические вероятности».