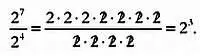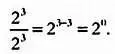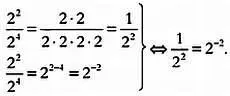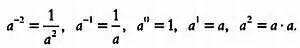Микель Альберти - Мир математики. т.20. Творчество в математике. По каким правилам ведутся игры разума

1 0,037563856636663…

2 0,919688568847383…

3 0,155382300008691…

4 0,000000033433002…

5 0,999995885994382…

6 0,101001000100001…

7 0,774647746477464…

…

Мы можем записать вещественное число вида 0, … не представленное в этом списке. Составить его можно так: если первый знак первого числа в списке равен 1, мы запишем 0, в противном случае — 1. Согласно этому правилу и с учетом вышеприведенных чисел наше новое число будет начинаться с 0,1…

Применим это же правило ко второму знаку второго числа в списке. Если он равен 1, мы запишем 0, в противном случае — 1. В записи нашего числа уже два знака: 0,10…

Повторим эти же рассуждения для следующих знаков числа. Для вышеприведенного списка наше число будет записываться так:

Ψ = 0,1011101…

Это число будет отличаться от всех присутствующих в списке как минимум одним знаком. Следовательно, этого числа в списке нет. По сути, найти его нам поможет сам список. Следовательно, составить исчерпывающий список невозможно, и вещественные числа в интервале от 0 до 1 сосчитать нельзя.

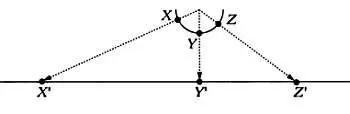
Доказательство Кантора показывает, что бесконечное множество вещественных чисел имеет иную природу, чем бесконечное множество натуральных, и это приводит к нескольким парадоксам. Например, несмотря на то что длина вещественной прямой и длина окружности произвольного радиуса отличаются, они содержат одинаковое число точек. Это может показаться бессмысленным, однако составим простую схему: если мы проведем из центра окружности все возможные лучи, которые пересекут окружность, то установим взаимно однозначное соответствие между точками полуокружности ( X, Y, Z , …) и точками вещественной прямой ( X', Y', Z' , …).

Все мы рассматриваем новые идеи через призму своего культурного опыта, и чтобы усвоить что-то новое, требуется взглянуть на уже известное под другим углом. Обучаясь, человек может обнаружить, что его рассуждения и рассуждения, приводимые в учебнике, вступают в конфликт друг с другом. Так происходит при изучении степеней, показатели которых являются отрицательными числами, десятичными дробями или иррациональными числами — их сложно понять в рамках классического подхода, где рассматриваются, например, операции умножения или деления.

Возвести число в степень означает умножить его на само себя столько раз, сколько указывает показатель степени:

3 4= 3·3·3·3

При перемножении степеней их показатели складываются, при делении — вычитаются:

2 3·2 5 = (2·2·2)·(2·2·2·2·2) = 2 8.

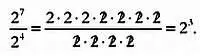
Однако если мы разделим друг на друга степени с одинаковым показателем, например, 2 3на 2 3, то получим удивительный результат. С одной стороны, он будет равен 1, так как 8/8 = 1. Но в соответствии с правилом показатели степеней должны вычитаться:

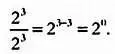
Это означает, что приведенный выше результат возможен только в том случае, если 2 0= 1. Но почему число, умноженное само на себя ноль раз, равно 1? И это не все. Если при делении степеней показатель в знаменателе больше, чем в числителе, то мы получим степень с отрицательным показателем:

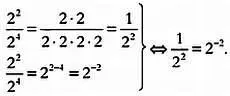
Изначально возведение числа в степень означало умножение этого числа на само себя несколько раз. Затем в математике появились операции и выражения, противоречащие этой точке зрения. Возвести число в отрицательную степень означает разделить единицу на число, умноженное само на себя столько раз, сколько указывает показатель степени. Логично ли это? Имеет ли это смысл? Да, это логично, но смысл этой операции нужно изменить. Нужно изменить понятие показателя степени как числа, означающего число сомножителей в произведении. Кроме того, степень с отрицательным показателем — то же самое, что степень с положительным показателем в знаменателе дроби. Таким образом:

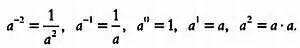
Подобным же образом описываются степени с дробными показателями. Если квадратный корень числа возвести в квадрат, то результатом будет исходное число: