Бизенц Торра - Том 15. От абака к цифровой революции. Алгоритмы и вычисления

* * *

ГОТФРИД ВИЛЬГЕЛЬМ ЛЕЙБНИЦ (1646–1716)

Немецкий мыслитель Готфрид Вильгельм Лейбниц вместе с Декартом и Спинозой входит в тройку великих рационалистов XVII века. Он был математиком, логиком, философом, геологом, историком и экспертом в юриспруденции. Он также внес огромный вклад в технологию и предвосхитил появление многих понятий в биологии, медицине, психологии и даже информатике. Независимо от Ньютона он создал анализ бесконечно малых. Введенные им обозначения используются и сейчас.

Составить полный перечень его открытий невозможно, поскольку до сих пор не издано полное собрание всех его сочинений, разбросанных по дневникам, письмам и рукописям, некоторые из которых никогда не публиковались. Лейбниц установил соответствие между двоичной системой счисления и сотворением мира: в его математическом представлении космоса, напоминавшем пифагорейское, ноль обозначал пустоту, единица — Бога.

* * *

В этой работе прослеживается влияние Раймунда Луллия: при написании «Рассуждения о комбинаторном искусстве» ( Dissertatio de Arte Combinatoria ) Лейбниц вдохновлялся его «Великим искусством». Для Лейбница даже приближение к божественному знанию должно было достигаться исключительно путем комбинирования основных понятий. Эти основные понятия, которым невозможно дать определение, должны были выражаться на языке математики. На их основе с помощью четких дедуктивных правил должны были выводиться различные истинные высказывания.

Лейбниц считал, что между логикой, математикой и метафизикой существует тесная взаимосвязь. Он был убежден, что его метафизика полностью математическая и что истинную метафизику сложно отличить от истинной логики.

Новые выражения для вычисления числа π

В течение XVII века различные исследователи предпринимали попытки вычислить значение π с помощью бесконечных рядов, следуя путем, который наметил Франсуа Виет. Одним из них был англичанин Джон Валлис(1616–1703) из Оксфордского университета. В своей книге «Арифметика бесконечного», опубликованной в 1633 году, Валлис описал различные выражения для вычисления интегралов и, взяв их за основу, получил следующее выражение для числа π :

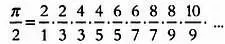
Математик и философ Уильям Броункер(1620–1684) , основатель и первый президент Лондонского королевского общества, путем преобразования этого выражения в 1658 году получил следующую формулу:

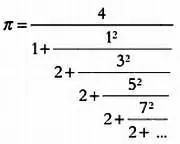
Следующее выражение, известное в Европе, было открыто за ее пределами. Речь идет о формуле Мадхавы из Сангамаграма. Лейбниц повторно открыл ее в 1671 году, использовав разложение в ряд для функции арктангенса, полученное Джеймсом Грегори. Она выглядит так:

π /4 = 1–1/3 + 1/5 — 1/7 + … + (-1) n /(2 n + 1) + …

и выводится из следующего разложения в ряд для арктангенса:

arctg x = х — ( x 3)/3 + ( х 5)/5 — ( х 7)/7 + …

XVIII век остался в истории веком Просвещения. Целью этой книги ни в коей мере не является критика Просвещения, однако нет сомнений в том, что в XVIII веке не было сделано значимых открытий в области исчисления и счета. Возможно, в XVII веке был совершен столь крупный прорыв в науке, что в последующем столетии ученые занимались исключительно изучением уже открытого ранее. Как бы то ни было, вычисления, логика и расчеты числа 71 в этот период следовали по пути, очерченному в XVII веке.

Вычисление числа π в XVIII веке

В XVIII веке было предложено несколько новых выражений для вычисления числа π . Первое из них получил астроном Джон Мэчин(1680–1751) . Оно использовалось для вычисления π в течение нескольких веков, в том числе при компьютерных вычислениях. Использовав формулу Грегори, Лейбница и Мадхавы, Мэчин обнаружил, что угол, арктангенс которого равен 1/5, можно выразить так:

α = arctg(1/5) = (1/5) — ((1/5) 3)/3 + ((1/5) 5)/5 — ((1/5) 7)/7 +…

На основе арктангенса угла (4 α — π /4) он составил ряд, позволяющий вычислить число π , в котором используется функция, обратная котангенсу. В отличие от предыдущих, этот ряд сходился быстрее. С его помощью этому английскому математику удалось верно вычислить 100 знаков числа π . Этот ряд соответствовал следующему выражению: