Теория множеств
Чтобы понять, в чем заключается парадокс, который положил конец счастливой и спокойной жизни Бертрана Рассела, сначала в нескольких словах опишем основы теории множеств. В предыдущей главе мы хотели показать, что основы аксиоматического метода можно встретить уже в «Началах», однако для Евклида аксиомы были очевидными истинами, а не исходными утверждениями, выбранными из соображений удобства. Со временем языка Евклида оказалось недостаточно для изложения новых математических идей. Доказать сложные теоремы XIX века исключительно с помощью слов и фигур было так же сложно, как сегодня перевести на один из мертвых языков инструкцию для iPhone.
Постепенно математическая нотация становилась все более символической: была введена форма, пригодная не только для записи рядов, производных и интегралов, — благодаря работам английского математика Джорджа Буля(1815–1864) стало возможным записывать в виде уравнений логические высказывания. Геометрия изучает фигуры в пространстве, арифметика — числа, математический анализ — средства, необходимые для формализации физических законов, алгебра — уравнения. Можно ли найти язык, общий для всех этих дисциплин, который сделал бы очевидным их единство?
* * *
БУЛЕВА АЛГЕБРА
Джордж Буль был первым, кто провел аналогию между логическими связками «и» и «или» и операциями умножения и сложения в алгебре. Он также ввел обозначения 0 («ложь») и 1 («истина») для двух значений логических переменных. Перед тем как рассмотреть пример, напомним, что при умножении чисел результат равняется нулю только тогда, когда одно из этих чисел равно нулю.
Допустим, что мы хотим перевести на язык алгебры высказывание «Все люди смертны».
Буль предложил обозначить через р значение истинности высказывания «быть человеком», за q— значение высказывания «быть смертным». Этот хитроумный прием позволяет свести содержание фразы к уравнению р·( 1— q) = 0.
Так, если некто является человеком, то рпринимает значение истинности 1 («истина»).
Уравнение гласит, что произведение чисел р и (1 — q) равно нулю. Так как р отлично от нуля, то 1 — qдолжно равняться нулю. Однако это означает, что q равно 1 («истина»), то есть что человек смертен.

Джордж Буль, один из прародителей вычислительной алгебры.
* * *
Размышляя о проблеме, которая изначально не имела ничего общего с этим скорее философским, нежели математическим вопросом, Георг Кантор в период с 1878 по 1884 год считал, что нашел ответ в теории множеств. На интуитивном уровне множество определяется как совокупность объектов: мы говорим о множестве животных, множестве парков Парижа или множестве читателей этой книги.
Эти совокупности можно определить, перечислив все входящие в них элементы либо указав нечто общее для этих элементов. Так, множество натуральных чисел (напомним, что натуральные числа — это числа, которые мы используем при счете) — это не что иное, как множество 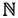 = {0, 1, 2, 3 …}. Если бы мы хотели рассмотреть только четные числа, то записали бы 2
= {0, 1, 2, 3 …}. Если бы мы хотели рассмотреть только четные числа, то записали бы 2 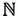 = {0, 2, 4, 6 …} или n кратно 2}, где символ
= {0, 2, 4, 6 …} или n кратно 2}, где символ 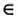 обозначает «принадлежит», а вертикальная черта |— «такое, что». Мы указали не список элементов множества, а правило его определения, так как в этом случае мы рассматриваем подмножество натуральных чисел, обладающее свойством делимости на два.
обозначает «принадлежит», а вертикальная черта |— «такое, что». Мы указали не список элементов множества, а правило его определения, так как в этом случае мы рассматриваем подмножество натуральных чисел, обладающее свойством делимости на два.
Едва начав работу, Кантор осознал, что в его новой теории рассматривались одновременно два объекта совершенно разной природы: конечные и бесконечные множества. По сути задача о нахождении числа элементов множества (математики называют его кардинальным числом, или мощностью множества) имеет разные решения в зависимости от того, конечное или бесконечное множество мы рассматриваем. Представим очень простую ситуацию: допустим, мы хотим узнать, имеют ли два конечных множества одно и то же кардинальное число, например равно ли число букв в слове «нахальство» числу цветов радуги. Очевидный метод заключается в том, чтобы подсчитать элементы каждого множества и сравнить результаты: так как в слове Н-А-Х-А-Л-Ь-С-Т-В-О десять букв, а в радуге семь цветов (красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый), то эти два множества содержат разное число элементов. Но что произойдет, если мы применим этот же метод к двум бесконечным множествам? В этом случае необходимо либо считать, что все бесконечные множества обладают одинаковым кардинальным числом и поставить на этом точку, либо использовать какой-то другой метод.
Читать дальше


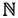 = {0, 1, 2, 3 …}. Если бы мы хотели рассмотреть только четные числа, то записали бы 2
= {0, 1, 2, 3 …}. Если бы мы хотели рассмотреть только четные числа, то записали бы 2 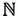 = {0, 2, 4, 6 …} или n кратно 2}, где символ
= {0, 2, 4, 6 …} или n кратно 2}, где символ 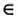 обозначает «принадлежит», а вертикальная черта |— «такое, что». Мы указали не список элементов множества, а правило его определения, так как в этом случае мы рассматриваем подмножество натуральных чисел, обладающее свойством делимости на два.
обозначает «принадлежит», а вертикальная черта |— «такое, что». Мы указали не список элементов множества, а правило его определения, так как в этом случае мы рассматриваем подмножество натуральных чисел, обладающее свойством делимости на два.










