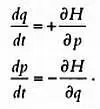Необходимо помнить, что кинетическая и потенциальная энергия зависит от импульсов и положений, которые, в свою очередь, являются временными функциями.
Найдем, как зависят положение и импульс от времени. Другими словами, мы хотим узнать, куда и с какой скоростью движется изучаемое тело. Используя уравнения Эйлера — Лагранжа, Гамильтону удалось изменить их так, чтобы найти новые равенства, зависящие только от гамильтониана. Открытые ученым уравнения могут быть выражены следующим образом:
— изменение положения во времени равно изменению гамильтониана за единицу импульса;
— изменение импульса во времени противоположно изменению гамильтониана в пространстве.
Ниже приведено их математическое выражение, в котором символы d и 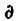 , несмотря на то что их значения немного различаются (не станем углубляться в эти различия), могут читаться как «изменение»:
, несмотря на то что их значения немного различаются (не станем углубляться в эти различия), могут читаться как «изменение»:
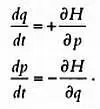
Говоря об уравнениях Гамильтона, следует отметить некоторые моменты. Во-первых, как и можно было ожидать, мы видим два уравнения вместо одного, поскольку теперь мы должны вычислить изменение как положения, так и импульса.
Во-вторых, уравнения не зависят от скорости, а только от импульса, положения и гамильтониана, как этого и хотел Гамильтон. Наконец, оба уравнения симметричны, кроме знака. Это совпадение кажется почти волшебным: как может быть, что положение и импульс, абсолютно разные величины, ведут себя так похоже? Это совпадение не давало покоя нескольким поколениям физиков, особенно после того, как было открыто, что подобное отношение — фундаментальная часть квантовой механики. В теории струн дуализм импульса и положения привел к еще более важному утверждению: можно математически описать вселенные, где импульс ведет себя так, как будто является положением, в то время как положение играет роль импульса, что было названо Т-дуализмом .
Применение уравнений Гамильтона
Применение уравнений Гамильтона открывает широкие возможности, благодаря чему сегодня эти уравнения используются не только в классической механике, для которой они были разработаны. Если законы Ньютона в релятивистской системе, где скорость частиц приближается к скорости света, перестают действовать, то уравнения Гамильтона продолжают давать верные результаты: надо лишь заново определить значения кинетической и потенциальной энергии. Уравнения Гамильтона можно считать основой супертеории в том смысле, что они охватывают частную физическую теорию и применяются для тел в электрических или гравитационных полях. Эти уравнения могут быть применены к любой еще не открытой силе при одном условии: необходимо вычислить связанную с ней потенциальную энергию.
Квантовая механика — это физическая теория, которая рассматривает процессы в микромире. В отличие от релятивистской механики, здесь уравнения Гамильтона перестают работать, поскольку все изменения положений и импульсов в микромире в некотором роде случайны. И все же гамильтониан в этой теории становится еще более важным, поскольку определяет изменение любой квантовой системы во времени. Особое отношение между положением и импульсом является ключевым для такого понятия, как принцип неопределенности, который гласит, что невозможно одновременно точно измерить и импульс, и положение частицы.
Математический аппарат, предложенный Гамильтоном почти 200 лет назад, работает и сегодня. Потенциал уравнений Гамильтона очень высок, и они используются в дисциплинах, мало связанных с физикой. Так, Давид Касс(1937–2008) , профессор экономики Пенсильванского университета, использовал эти уравнения для создания модели экономического роста. Он сопоставил значения импульсов, положений и некоторых экономических переменных, таких как экономический поток или цены, чтобы с помощью гамильтониана создать модель валового внутреннего продукта государства. Конечной целью Касса была возможность прогнозировать и даже направлять экономическое развитие. Ученые продолжают адаптировать уравнения Гамильтона для многих других отраслей.
До сих пор мы приводили только примеры применения уравнений Гамильтона к одной частице, но благодаря гибкой формулировке этот инструмент позволяет работать с неограниченным их числом. Анализ систем из нескольких частиц — это первый шаг к пониманию газовой динамики.
Читать дальше

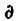 , несмотря на то что их значения немного различаются (не станем углубляться в эти различия), могут читаться как «изменение»:
, несмотря на то что их значения немного различаются (не станем углубляться в эти различия), могут читаться как «изменение»: