Площади сечений таковы:
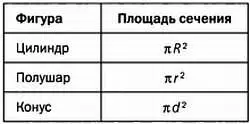
Так как r 2+ d 2= R 2, имеем:
Площадь сечения цилиндра= Площадь сечения полушара+ Площадь сечения конуса.
Сечения фигуры подобны ломтям хлеба: если для каждого сечения выполняется приведенное выше соотношение, то кажется вполне очевидным, что это же отношение будет выполняться и для объемов фигур. Иными словами,
Объем цилиндра= Объем полушара+ Объем конуса.
Архимед знал, как вычисляется объем цилиндра и объем конуса:
V (цилиндра) = πR 3; V (конуса) = 1/ πR 3.
Он получил равенство
V (полушара) = V (цилиндра) — V (конуса) = πR 3— (1/3) πR 3= 2 πR 3/3
Таким образом,
V (сфера) = 4 πR 3/3.
И вновь задачи о вычислении объемов были окончательно решены с появлением дифференциального исчисления. Рассмотрим в качестве примера, как с его помощью вычисляется объем шара радиуса г. Начнем с того, что приведем уравнение окружности
х 2+ у 2= r 2.
Вращая полукруг вокруг оси абсцисс, получим шар.
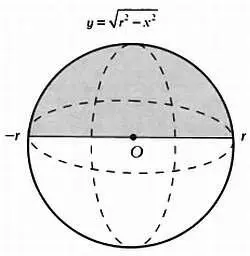
Шар, полученный вращением полукруга.
Объем тела вращения, полученного вращением плоской фигуры, ограниченной линиями у = f( x ), у = 0, х = а и х = Ь , вокруг оси ОХ , вычисляется по формуле:
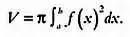
Эта формула в некотором роде отражает метод Архимеда, если интерпретировать π f( x ) 2как площадь круга и представить, что тело вращения, как в примере Архимеда, состоит из «ломтей»-сечений. Напомним, что 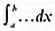 обозначает интеграл — сумму объемов бесконечного числа сечений бесконечно малой толщины ( dx ), которые составляют объем тела вращения. В нашем примере
обозначает интеграл — сумму объемов бесконечного числа сечений бесконечно малой толщины ( dx ), которые составляют объем тела вращения. В нашем примере
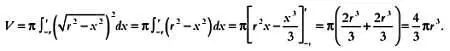
Понятие меры появилось свыше 5 тысяч лет назад, когда возникла необходимость в измерении предметов, окружавших человека. Посмотрим, какими были основные задачи, стоявшие перед математиками конца XIX века и приведшие к созданию теории меры. Древние египтяне занимались вычислением площадей и объемов (см. папирус Ахмеса и Московский математический папирус) и использовали приближенное значение π 4(1 – 1/9) 2= 3,160…, однако строгие доказательства формул для вычисления площадей и объемов привели не они, а уже древнегреческие математики.
Эти доказательства даны в «Началах» Евклида (ок. 300 г. до н. э.), где, однако, нет определений длины, площади и объема — эти понятия определяются неявно при описании фигур. Так, определяется линия, поверхность и тело: линия есть длина без ширины, поверхность — то, что имеет лишь длину и ширину, а тело — то, что имеет длину, ширину и глубину. Евклид также не определил, что означает «измерить» — это слово он использует не только в связи с тремя вышеупомянутыми «величинами», но и по отношению к числам. К примеру, он определяет «часть» и «части» аналогично современным понятиям «делитель» и «не делитель», но использует при этом слово «измерить: «Часть есть число в числе, меньшее в большем, если оно измеряет большее. Части же — если оно его не измеряет». Так, к примеру, 3 — «часть» 13, а 6 — «части» 13.
Не встретим мы определения меры и у других древнегреческих авторов, в частности у Архимеда, который сравнивает известные площади и объемы для вычисления новых. Так, мы показали, как он вычислил объем шара. Подобных понятий меры было достаточно для развития математики на протяжении многих веков.
Главным героем следующего этапа стал Георг Кантор(1845–1918) , который в 1883 году дал первое определение меры m( А ) произвольного (ограниченного) множества  . Кроме того, Кантор обнаружил, что не все бесконечные множества имеют одинаковые размеры, то есть одинаковую мощность: к примеру, множество рациональных чисел является счетным, то есть имеет тот же размер, что и множество натуральных чисел, а множество вещественных чисел — нет. В этом смысле измерить означает установить взаимно-однозначное соответствие (на языке математики — биекцию) между двумя множествами, одним из которых будет
. Кроме того, Кантор обнаружил, что не все бесконечные множества имеют одинаковые размеры, то есть одинаковую мощность: к примеру, множество рациональных чисел является счетным, то есть имеет тот же размер, что и множество натуральных чисел, а множество вещественных чисел — нет. В этом смысле измерить означает установить взаимно-однозначное соответствие (на языке математики — биекцию) между двумя множествами, одним из которых будет  (множество натуральных чисел) или одна из его степеней ( x , x x и так далее). К примеру, для множества рациональных чисел можно установить следующее соотношение:
(множество натуральных чисел) или одна из его степеней ( x , x x и так далее). К примеру, для множества рациональных чисел можно установить следующее соотношение:
Читать дальше



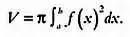
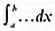 обозначает интеграл — сумму объемов бесконечного числа сечений бесконечно малой толщины ( dx ), которые составляют объем тела вращения. В нашем примере
обозначает интеграл — сумму объемов бесконечного числа сечений бесконечно малой толщины ( dx ), которые составляют объем тела вращения. В нашем примере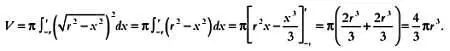
 . Кроме того, Кантор обнаружил, что не все бесконечные множества имеют одинаковые размеры, то есть одинаковую мощность: к примеру, множество рациональных чисел является счетным, то есть имеет тот же размер, что и множество натуральных чисел, а множество вещественных чисел — нет. В этом смысле измерить означает установить взаимно-однозначное соответствие (на языке математики — биекцию) между двумя множествами, одним из которых будет
. Кроме того, Кантор обнаружил, что не все бесконечные множества имеют одинаковые размеры, то есть одинаковую мощность: к примеру, множество рациональных чисел является счетным, то есть имеет тот же размер, что и множество натуральных чисел, а множество вещественных чисел — нет. В этом смысле измерить означает установить взаимно-однозначное соответствие (на языке математики — биекцию) между двумя множествами, одним из которых будет  (множество натуральных чисел) или одна из его степеней ( x , x x и так далее). К примеру, для множества рациональных чисел можно установить следующее соотношение:
(множество натуральных чисел) или одна из его степеней ( x , x x и так далее). К примеру, для множества рациональных чисел можно установить следующее соотношение:










