Приближенное значение S рассчитывается как сумма гипотенуз:

Чем меньше будет длина этих n отрезков, тем точнее будет полученный результат. В пределе все Δх i будут стремиться с нулю, и, согласно определению определенного интеграла, на отрезке между а и Ь мы получим приведенную выше формулу:

Квадратура
Квадратура — построение квадрата, по площади равного данной фигуре. Исторически сложилось, что квадратом называется вторая степень числа, то есть число, умноженное на само себя. Схожесть этих терминов неслучайна — если возвести число во вторую степень, то есть умножить его на само себя, то мы найдем площадь квадрата, сторона которого выражается этим числом.
На следующем рисунке показано, как при возведении во вторую степень выражения ( а + Ь ) получается площадь квадрата со стороной а + Ь :
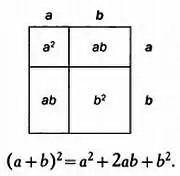
Здесь следует провести различие между площадью и поверхностью, так как эти понятия иногда путают. Поверхность — геометрический термин, площадь — величина, соответствующая этому геометрическому термину, то есть мера протяженности поверхности, выраженная в соответствующих единицах.
Кроме того, некоторые порой путают периметр и площадь. Их следует различать подобно тому, как различают окружность и круг. Периметр (от латинского perimetros , произошедшего от греческого 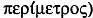 это граница поверхности или фигуры, а также длина этой границы, а площадь — это мера, или численная характеристика, поверхности или фигуры, ограниченной периметром. Возникает вопрос: если задан определенный периметр, например дана веревка заданной длины, то каким будет прямоугольник наибольшей площади, который можно ограничить этой веревкой? Этот вопрос можно сформулировать и в более общем виде: как будет выглядеть фигура наибольшей площади, которую можно ограничить этой веревкой?
это граница поверхности или фигуры, а также длина этой границы, а площадь — это мера, или численная характеристика, поверхности или фигуры, ограниченной периметром. Возникает вопрос: если задан определенный периметр, например дана веревка заданной длины, то каким будет прямоугольник наибольшей площади, который можно ограничить этой веревкой? Этот вопрос можно сформулировать и в более общем виде: как будет выглядеть фигура наибольшей площади, которую можно ограничить этой веревкой?
Ответом на первый вопрос будет квадрат, на второй вопрос — круг. Ответы на эти вопросы известны с глубокой древности и применяются в повседневной жизни множеством способов. В главе 1 мы упомянули, что традиционные жилища в самых разных культурах (у инуитов, североамериканских индейцев и аборигенов Кении) имели круглую форму — так обеспечивалась наибольшая площадь при минимальном расходе материала.
Парадоксально, но определенные фигуры имеют конечную площадь, но бесконечный периметр. К примеру, это справедливо для фрактала под названием снежинка Коха, который представляет собой непрерывную кривую, но задается функцией, не дифференцируемой ни в одной точке. Эту кривую описал шведский математик Хельге фон Кох(1870–1924) в 1904 году. Из четырех отрезков равной длины (например, 1), соединенных так, как показано на первом рисунке внизу ( KQ ), строится кривая Коха, на основе которой определяется снежинка Коха.
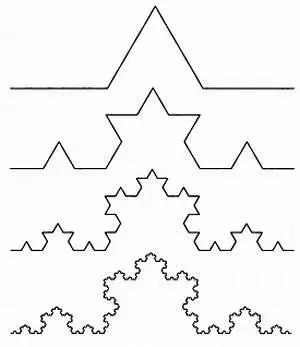
Четыре первых этапа построения кривой Коха. Сверху вниз: К 0, K 1, К 2 и К 3.
На первом этапе все 4 отрезка К 0 заменяются копией К 0 уменьшенной в 3 раза. Полученная кривая (обозначим ее K 1 ) будет состоять из 16 = 4 2отрезков. Далее заменим каждый из этих 16 отрезков копией K 1 , уменьшенной в З 2= 9 раз. Полученная кривая (обозначим ее К 2 ) будет состоять из 64 = 4 3 отрезков, и так далее. Кривая Коха определяется как предел последовательности К i при i , стремящемся к бесконечности.
Для построения снежинки Коха возьмем 3 копии K 0 , расположим их в форме равностороннего треугольника и заменим его стороны описанными выше кривыми.

Снежинка Коха.
Снежинка Коха имеет конечную площадь, но бесконечный периметр. Ее площадь конечна потому, что фигура умещается внутри круга конечного радиуса. В нашем примере длина исходных отрезков кривой K 0 равна 1, и можно доказать, что снежинка умещается внутри круга радиуса 3. Чтобы доказать, что снежинка Коха имеет бесконечный периметр, достаточно показать, что кривая Коха имеет бесконечную длину. Для этого вычислим длину l( К i ) на каждом шаге построения. Длина K 0 равна 4 (4 стороны длиной 1). Так как К 1 состоит из 16 = 4 2 отрезков длиной 1/3, длина этой кривой будет равна:
Читать дальше




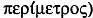 это граница поверхности или фигуры, а также длина этой границы, а площадь — это мера, или численная характеристика, поверхности или фигуры, ограниченной периметром. Возникает вопрос: если задан определенный периметр, например дана веревка заданной длины, то каким будет прямоугольник наибольшей площади, который можно ограничить этой веревкой? Этот вопрос можно сформулировать и в более общем виде: как будет выглядеть фигура наибольшей площади, которую можно ограничить этой веревкой?
это граница поверхности или фигуры, а также длина этой границы, а площадь — это мера, или численная характеристика, поверхности или фигуры, ограниченной периметром. Возникает вопрос: если задан определенный периметр, например дана веревка заданной длины, то каким будет прямоугольник наибольшей площади, который можно ограничить этой веревкой? Этот вопрос можно сформулировать и в более общем виде: как будет выглядеть фигура наибольшей площади, которую можно ограничить этой веревкой?












