Иоланда Гевара - Том 38. Измерение мира. Календари, меры длины и математика

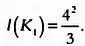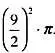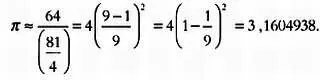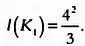
Обобщив рассуждения, получим:

* * *

УЧАСТОК НАИБОЛЬШЕЙ ПЛОЩАДИ, ПОКРЫТЫЙ БЫЧЬЕЙ ШКУРОЙ

У Маттона, царя Тира, было двое детей — Пигмалион и Элисса (таким было тирское имя царицы Дидоны). После смерти Мапона трон занял его сын Пигмалион, еще ребенок. Элисса, подстрекаемая Пигмалионом, вышла замуж за его дядю Сикарба, жреца храма Геракла и второго человека в государстве после самого царя, так как Пигмалион хотел заполучить сокровища, спрятанные Сикарбом. Спустя некоторое время Пигмалион попросил Элиссу разузнать, где муж прячет сокровища. Она подчинилась, но не сказала брату, где находится тайник. Пигмалион повелел убить Сикарба, чтобы завладеть его богатством, а Элисса успела скрыться на корабле вместе со знатными тирийцами, захватив сокровища с собой. Беглецы высадились на севере Африки, где их тепло приняли местные жители, заключившие с прибывшими договор: тирийцам разрешалось занять столько земли, сколько можно было покрыть бычьей шкурой. Те разрезали шкуру на очень тонкие ремни, связали их вместе и опоясали ими достаточно большой участок. Местные жители в соответствии с договором передали им землю, где был основан город. Новый город получил название Бирса, что по-финикийски означает «бычьи шкуры». Спустя некоторое время царь соседнего племени Иарбант захотел жениться на Дидоне и угрожал объявить войну в случае отказа. Дидона отказалась и покончила с собой. На основе этой легенды Вергилий создал «Энеиду» — поэму о похождениях троянского героя Энея. Корабль Энея прибивает бурей к побережью Африки, и его подбирают жители Карфагена — города, основанного Дидоной. Дидона влюбляется в Энея и умоляет его остаться. Тот отказывается, и Дидона кончает жизнь самоубийством.

«Эней рассказывает Дидоне о несчастьях Трои». Картина французского художника Пьер-Нарцисса Герена.

* * *

При спрямлении мы измеряли длину морского побережья при помощи смоченной нити, наложенной на карту. Аналогичным образом можно вычислять и площади поверхностей. Для этого нам потребуется прозрачный лист бумаги, разделенный на квадраты. Подсчитав число квадратов, покрывающих поверхность, и зная масштаб изображения, можно с хорошей точностью определить искомую площадь.

С древних времен одной из самых знаменитых задач о квадратуре была задача о квадратуре круга. Она заключается в том, чтобы с помощью циркуля и линейки построить квадрат, по площади равный данному кругу.

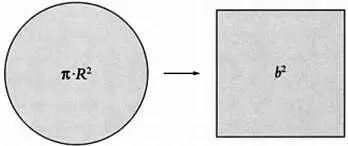
Площадь круга должна быть равна площади построенного квадрата.

Папирус Ахмеса (также известный как папирус Ринда по имени его владельца Генри Ринда, который приобрел его в 1858 году), обнаруженный при строительстве здания в Луксоре, был написан писцом по имени Ахмес примерно в 1650 году до н. э. и содержит информацию из периода 2000 год до н. э. — 1800 год до н. э. В задаче 48 площадь круга диаметром в 9 единиц принимается равной площади восьмиугольника, вписанного в квадрат с длиной стороны в 9 единиц, как показано на рисунке.

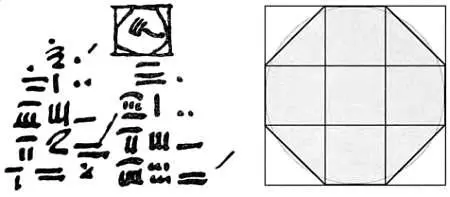
Фрагмент папируса Ахмесаи рассматриваемый восьмиугольник.

Площадь круга равна: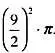

Приближенное значение площади многоугольника принимается равным 64. В действительности оно составляет 63, так как площадь каждого квадрата равна 3 х 3 = 9, а многоугольник состоит из 5 целых квадратов и 4 половин — всего 7 квадратов площадью в 9 единиц каждый. В расчетах мы будем использовать значение площади в 64 единицы, так как 64 — квадрат (8 2). Кроме того, так мы сможем использовать только дроби с числителем, равным 1, подобно древним египтянам.

Так, ~= 64. Проведя необходимые расчеты и упростив выражение, получим:

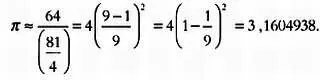
Задача о квадратуре круга наряду с задачами об удвоении куба и трисекции угла принадлежала к числу трех классических задач древнегреческой математики. Задача о вычислении квадратуры плоских поверхностей, ограниченных кривыми, вызвала бы у греков довольно много трудностей, если бы Гиппократ Хиосский(ок. 470 г. до н. э. — ок. 410 г. до н. э.) не доказал, что возможно вычисление квадратуры определенных криволинейных фигур — двуугольников, построенных особым образом.