Хавьер Арбонес - Том 12. Числа-основа гармонии. Музыка и математика

Факториал любого целого положительного числа п определяется как произведение всех целых положительных чисел от 1 до n. Таким образом, n! = n·( n— 1)·…·2·1.

Однако для додекафонических серий подсчет «различных по сути» мелодий выглядит несколько сложнее, так как в этом случае не должны учитываться транспозиции, инверсии, ракоходы и сочетания этих преобразований. Тщательные подсчеты показывают, что число различных серий равно 9 985 920.

* * *

Числовая и матричная форма

Традиционные партитуры, в которых используется нотный стан, подчиняются логике диатонической музыки. Одним из следствий этого является тот факт, что расстояние между соседними линиями нотного стана и промежутками между ними не всегда обозначает один и тот же музыкальный интервал. Иногда этот интервал состоит из двух полутонов (от ре до ми ), иногда — из одного (от ми до фа ). Из-за этого в додекафонической музыке используются альтерации. По этой причине, как видно из предыдущих примеров, инверсии и ракоходы додекафонических серий «не видны» на партитурах.

Серию также можно представить в числовом виде, что упрощает запись мелодии. При записи серий в числовом виде, как правило, выбирается исходная нота. В следующем примере исходной нотой является ми , которой присвоено значение 0. Далее последовательно нумеруются полутона: фа обозначается 1, фа диез — 2, соль — 3 и так далее.

При представлении серии в числовом виде для нахождения связанных серий можно использовать средства арифметики. Например, транспозиция серии получается прибавлением одного и того же числа k к каждому элементу серии:

T k ( s 1 , s 2 , …, s 12 ) —> ( s 1 + k , s 2 + k , …, s 12 + k ),

T 0 (0, 1, 3, 9, 2, 11, 4, 10, 7, 8, 5, 6) —> (0, 1, 3, 9, 2, 11, 4, 10, 7, 8, 5, 6),

T 1 (0, 1, 3, 9, 2, 11, 4, 10, 7, 8, 5, 6) —> (1, 2, 4, 10, 3, 0, 3, 11, 8, 9, 6, 7),

T 2 (0, 1, 3, 9, 2, 11, 4, 10, 7, 8, 5, 6) —> (2, 3, 5, 11, 4, 1, 6, 0, 9, 10, 7, 8),

…

T 7 (0, 1, 3, 9, 2, 11, 4, 10, 7, 8, 5, 6) —> (7, 8, 10, 4, 9, 6, 11, 3, 2, 3, 0,1),

…

T 12 (0, 1, 3, 9, 2, 11, 4, 10, 7, 8, 5, 6) —> (11, 0, 2, 8, 1, 10, 3, 9, 6, 7, 4, 5).

После 11 счет снова начинается с 0, точно так же как мы считаем часы: 8 часов утра плюс 7 часов равно 3 часам дня. В математике подобные операции на ограниченных множествах чисел называются модулярной арифметикой. В случае с додекафоническими сериями множество чисел имеет всего 12 элементов в интервале от 0 до 11. Число элементов множества называется модулем (в нашем случае модуль равен 12). В арифметике по модулю 12 число 13 эквивалентно числу 1. Записывается это так:

13 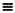1 (mod 12).

Все числа вида 12 k + 1, где k — целое, эквивалентны 1:

25 1 (mod 12),

37 1 (mod 12),

49 1 (mod 12),

61 1 (mod 12),

Как мы уже говорили, в додекафонии не проводятся различия между одинаковыми нотами, которые относятся к разным октавам. Арифметика по модулю 12 отражает этот факт: число 1, которым в нашем примере обозначена нота фа , равно 13, которым снова обозначается фа .

Средства модульной арифметики помогают заметить, что инверсия серии эквивалентна замене всех значений от 0 до 11 (то есть значений всех различных нот) разницей между этим значением и 12. При таком преобразовании значение 1 заменится на 11, 2 — на 10, 3 — на 9 и так далее. Для серии, которую мы рассматривали

в качестве примера, получим:

I ( s 1 , s 2 , .. ., s 12 ) —> ( s 1 , 12 — s 2 ,…, 12 — s 12 )

I (0,1, 3, 9, 2, 11, 4, 10, 7, 8, 5, 6) —> (0, 11, 9, 3, 10, 1, 8, 2, 5, 4, 7, 6).

Ракоход, в свою очередь, получается «обращением» числового ряда слева направо:

R ( s 1 , s 2 , ..., s 12 ) —> ( s 12 , s 11 , ..., s 1 )

R (0, 1, 3, 9, 2, 11, 4, 10, 7, 8, 5, 6) —> (6, 5, 8, 7, 10, 4, 11, 2, 9, 3, 1, 0).

Исходная серия вкупе с ее инверсией, ракоходом и с 12 возможными транспозициями для каждого из этих преобразований формирует 4·12 = 48 перестановок, которые может использовать композитор. Если учитывать повороты, то число вариантов возрастет до 48·12 = 576.

Эти 48 форм можно записать в виде матрицы размером 12 x 12, опираясь на следующие правила:

— в первой строке T 0 записывается исходная серия (в нашем примере выделена жирным шрифтом);

— в первом столбце I 0 записывается инверсия серии (также выделена жирным);

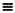— в каждой из оставшихся ячеек записывается сумма (по модулю 12) чисел, с которых начинаются соответствующая строка и столбец. Например, пятая строка начинается с числа 10, четвертый столбец с числа 9, следовательно, на пересечении этой строки и этого столбца необходимо записать число 7, так как 10 + 9 = 19 7 (mod 12).