Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

По окончании Второй мировой войны в Великобритании и США появились первые компьютеры. Два союзных государства начали борьбу за право называться их родиной, и толчком к началу этого соперничества стала возможность использования компьютеров прежде всего в военных целях. Новая техника создавалась для борьбы с общим врагом — СССР. Напомним, что именно эти годы стали началом эпохи холодной войны, и изменение политической обстановки повлияло на работы ученых во всем мире.

Хотя историки науки считают, что первый компьютер, известный как ENIAC ( Electronic Numerical Integrator and Computer — «электронный числовой интегратор и вычислитель»), был сконструирован в США в 1946 году, сегодня мы знаем, что до него существовал «Колосс», созданный в Великобритании в 1944 году.

В 1950 году Алан Тьюринг, один из самых плодовитых британских ученых XX столетия, сконструировал компьютер АСЕ (сокр. от англ. Automatic Computing Engine — «автоматическая вычислительная машина») в Национальной физической лаборатории. Этот компьютер имел возможности хранения данных и работы программ, весьма схожие с возможностями первых компьютеров Macintosh , созданных только в 1980-е годы. Компьютер Тьюринга был британским конкурентом американского EDVAC (от Electronic Discrete Variable Automatic Computer — «универсальный автоматический компьютер с дискретными переменными»), созданного на базе ENIAC. В конструировании EDVAC участвовал еще один гениальный ученый того времени — Джон фон Нейман.

«Колосс» — первый компьютер в истории, построенный в Великобритании в 1944 году.

Британским ответом на EDVAC стал EDSAC ( Electronic Delay Storage Automatic Computer — «электронный автоматический вычислитель с памятью на линиях задержки») — еще один компьютер с похожими характеристиками. В это же время в США был сконструирован UNIVAC ( Universal Automatic Computer — «универсальный автоматический компьютер») — прямой потомок ENIAC и EDVAC. Изготовившая его компания Remington Road стала первым в мире производителем коммерческих компьютеров.

Открытия Алана Тьюринга

В 1948 году в Университете Манчестера находился один из самых мощных компьютеров того времени, а в 1951 году университет получил компьютер Ferranti Mark I, на котором работал Тьюринг. С 1952 года до своей смерти в 1954 году Тьюринг был одним из первых ученых, кто использовал компьютер для математического моделирования биологических задач.

Компьютер Ferranti Mark I, на котором работал Алан Тьюринг(на фото справа, стоит).

В то время Тьюринга очень интересовало математическое изучение морфогенеза.

Одна из самых любопытных задач этой дисциплины заключается в том, чтобы объяснить, как живые организмы обретают конечную форму: почему ветви деревьев образуют именно такую структуру, почему членистоногие словно состоят из отдельных кусочков, а кольчатые черви — из колец. Еще одна классическая задача морфогенеза заключается в изучении узоров, например на коже некоторых позвоночных — полосок у зебр или круглых пятен у далматинцев.

Тьюринг первым попытался решить биологические задачи с помощью компьютера, став одним из пионеров вычислительной биоматематики. Таким образом, его исследования придали этой дисциплине более прикладной характер, сблизив ее с привычными биологическими исследованиями в лаборатории. Биологи и другие ученые под влиянием работ Тьюринга также начали изучать жизнь с математической точки зрения. Подобные исследования проводились в разные годы XX века; проводятся они и сейчас. Кроме того, Тьюринг открыл новую область математической биологии, предложив первую математическую теорию морфогенеза. В одной из своих работ для анализа формы растений он использовал числа Фибоначчи.

Последовательность Фибоначчи 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т. д. образуется по следующему правилу: если принять первое число Фибоначчи, a 1 , равным 0, второе число, a 2 , равным 1, то каждое последующее число будет определяться как сумма двух предыдущих. Иными словами, а n = а n-1 + а n-2 . Любопытно, что числа Фибоначчи описывают количество лепестков цветов, расположение чешуек шишек и листьев растений.

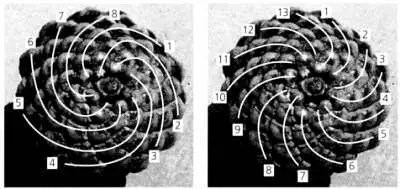
Число спиралей на этой шишке в каждом направлении (8 и 13 соответственно) выражается последовательными числами Фибоначчи.