| А |
НЕ А |
А И-НЕ В |
| 0 |
0 |
1 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
На следующей схеме показано, как соединить вентили И-НЕ между собой, чтобы получить вентили И и ИЛИ.
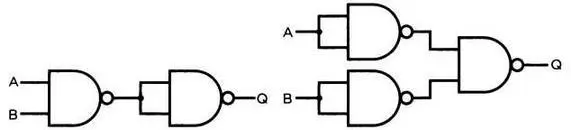
Взаимное соединение вентилей И-НЕ для получения вентиля И (слева) и вентиля ИЛИ (справа) со входами А, В и выходом Q.
В статье «Умные машины», одной из первых в мире работ по искусственному интеллекту, Алан Тьюринг использовал вентили И-НЕ для симуляции нейронных цепей, которые назвал нейронными цепями типа В.
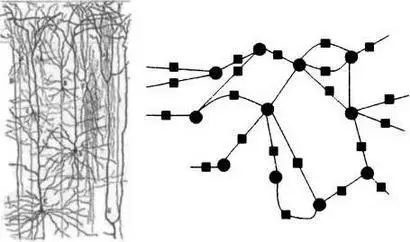
Нейронная сеть, изображенная Сантьяго Рамон-и-Кахалем (слева), и искусственная нейронная сеть (справа).
Эти волокна определяют конфигурацию нейронов: возбужденное состояние или нейтральное. В возбужденном состоянии, когда волокно Р активно, если модификатор связи получает на входе input 0 или 1, на выходе output будет возвращен тот же результат, 0 или 1 соответственно. С другой стороны, в нейтральном состоянии, когда волокно I активно, модификатор соединения будет вести себя так, что при любой величине на входе input, на выходе output результат всегда будет 1.
Кроме этих модификаторов, модель искусственного нейрона предполагала, что каждый нейрон имел два входа: ВХОД 1 и ВХОД 2 — и один ВЫХОД. Если оба входа находились в возбужденном состоянии, величина на ВЫХОДЕ получалась с применением булева оператора И-НЕ (вентиль И, выход которого соединяется с вентилем НЕ).
| ВХОД 1 |
ВХОД 2 |
выход |
| 0 |
0 |
1 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
Напротив, если ВХОД 1 находился в неактивном состоянии, величина на ВЫХОДЕ была равна обратной величине на ВХОДЕ 2, то есть 1, когда на ВХОДЕ 2 было 0 и наоборот.
| ВХОД 1 |
ВХОД 2 |
выход |
| 0 |
0 |
1 |
| 0 |
1 |
0 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
Если мы сравним модель искусственного нейрона Тьюринга с моделью Маккалока — Питтса, то увидим, что в последней величина на ВЫХОДЕ рассчитывается с заменой модификатора соединения на величину коэффициента w, который отражает синаптическую пластичность нейронов, то есть лучшую или худшую проходимость сигнала от одного нейрона к другому через синаптическую связь. Согласно формальной модели Маккалока — Питтса, нейрон ведет себя как калькулятор, способный вычислять сумму входных сигналов. Умножим каждый сигнал или ВХОД i на соответствующий коэффициент wi, сумму всех сигналов обозначим как ИТОГ:
ИТОГ = Σwi ВХОДi
После выполнения данной операции нейрон «решает», достаточна ли полученная информация ИТОГ для активации, или возбуждения. В самой элементарной модели нейрона величина ВЫХОДА получается с помощью ступенчатой функции:
1 ИТОГ ≥ U
ВЫХОД =
0 ИТОГ ≤ U
При этом величина порога U устанавливается предварительно. Обратим внимание, что эта величина показывает чувствительность нейрона к внешнему стимулу: нейрон более чувствителен, чем ближе к нулю величина ί, так как чем меньше порог, тем вероятнее, что ИТОГ превзойдет его величину при возбуждении нейрона. Если величина на ВЫХОДЕ равна нулю, нейрон останется в состоянии покоя, если на ВЫХОДЕ будет некоторая величина, нейрон перейдет в возбужденное состояние. При возбуждении нейрон отправляет ответ, величину 1, следующему нейрону, для которого это будет величина на ВХОДЕ. В других случаях величина 1 в комбинации с величинами на ВЫХОДЕ от других нейронов, например 1001, будет ответом нейронной сети на входящий сигнал.
ТЕСТ ТЬЮРИНГА
Тьюринг исследовал вопрос, как определить, разумно ли ведет себя машина (компьютер). Ученый очень изящно избежал необходимости дать определение разуму и принял следующую точку зрения: хотя машина не разумна в том смысле, в каком это относится к человеку, ее поведение может быть разумным.
Такая форма рассмотрения вопроса сегодня называется поведенческим подходом. Например, нам известно, что программы для игры в шахматы не являются разумными, но при игре они ведут себя так, будто они разумны. При этом Алан Тьюринг не дал определения разума и не ответил на вопрос, могут ли машины мыслить. На основе этих идей Тьюринг придумал испытание, известное как тест Тьюринга, состоящее в том, что машину, компьютер или программу, разумное поведение которой нужно оценить, подвергают следующей процедуре. Представим себе человека, у которого есть монитор и клавиатура. С их помощью он может задавать вопросы компьютеру, находящемуся в другой комнате. Ответ высвечивается на экране его монитора. Например, человек печатает на английском языке с помощью клавиатуры последнюю фразу, сказанную компьютером HAL-9000 в фильме «2001 год: Космическая одиссея»:
Читать дальше














