Rafael Lahoz-Beltra - Размышления о думающих машинах. Тьюринг. Компьютерное исчисление

Точка зрения Тьюринга на работу мозга в целом совпадала с идеями нейрофизиолога и кибернетика Уоррена Маккалока (1898-1969), а также логика и специалиста по когнитивной психологии Уолтера Питтса (1923-1969), которые в 1943 году представили модель искусственного нейрона, названную моделью Маккалока — Питтса. Она доказывала, что клетки, в особенности нейроны мозга, могут выполнять булевы операции, например вести себя как операторы И, ИЛИ и другие, — так же как и машины Тьюринга.

Описания настоящих моделей нейронов Тьюринга, Маккалока и Питтса стали предвестниками субсимвольного подхода к созданию ИИ. Согласно этой концепции, любой аспект ума или поведения человека и животных возникает, является следствием или объясняется взаимным соединением нейронов в нейронную сеть или цепь. Сегодня на основе субсимвольного подхода разрабатываются и программируются цепи искусственных нейронов — искусственные нейронные сети. В повседневной жизни эти сети широко используются, например при оптическом распознавании символов (OCR), номерных знаков автомобилей на парковках, сканировании, оптимизации расписаний, прогнозе изменения цен и кредитных рисков, распознавании данных на электроэнцефалограмме человека, классификации сигналов радара, разработке «умного» оружия и так далее.

Один из интересных опытов, который мы можем проделать с нейронами Маккалока — Питтса, — это использование их в качестве компонентов компьютера. В таком компьютере арифметические и логические операции будут выполняться внутри микропроцессора в арифметико-логическом устройстве (АЛУ). Нейронные цепи могут выполнять операции, схожие с компьютерными, с помощью логических вентилей, например И, ИЛИ, а также другие операции, свойственные биологическим нейронам. Процедура построения логического вентиля, выполняющего операцию булевой алгебры, начинается с определения соответствующих величин для коэффициентов соединений (w ±и w 2) и порога активации (U), как показано на схеме.

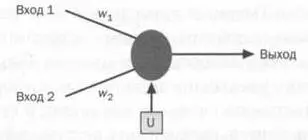
Комбинируя несколько искусственных нейронов, пошагово соединяя выходы одних со входами других, мы можем получить цепи, эмулирующие операторы И и ИЛИ. Однако можно сделать это проще, с одним нейроном Маккалока — Питтса. Эти простые опыты доказывают, что, как и думали Тьюринг, Маккалок и Питтс, нейрон является автоматом с двумя состояниями: активным, или возбужденным (1), и состоянием покоя (0), а также что нейронная цепь может выполнять функции, схожие с функциями арифметико-логического устройства (АЛУ) компьютера. Используем следующую программу на языке BASIC-256, чтобы показать, что нейрон будет вести себя как вентиль И при следующих входящих (О и 1) и исходящих сигналах.

rem Оператор И

els

wl=0.5:w2=0.5:u=0.5

input "вход 1 = ",el

input "вход 2 = ",e2

total=wl*el+w2*e2

if total <=u then

print "выход = 0"

else

print "выход = 1"

end if

С другой программой нейрон будет вести себя как вентиль ИЛИ.

rem Оператор ИЛИ

els

wl=l:w2=l:u=0.5

input "вход 1 = ",el

input "вход 2 = ",e2

total=wl*el+w2*e2

if total <=u then

print "выход = 0"

else

print "выход = 1"

end if

Итак, какой же была модель искусственного нейрона Алана Тьюринга? Представим, что нейрон — это круг, соединенный с другими кругами, символизирующими соседние нейроны. Добавим в местах соединений прямоугольник, который будет обозначать модификатор связи Тьюринга, дающий дезорганизованной машине типа В способность обучаться. Каждый модификатор связи имеет две линии, или «волокна тренировки», которые мы обозначим как Р и I.

Одним из практических аспектов цифровой электроники и следствием булевой алгебры является тот факт, что вентили И и ИЛИ могут получиться из вентиля И-НЕ (NAND), то есть вентиля И, выход которой трансформирован вентилем НЕ. Вентиль НЕ имеет единственный вход и единственный выход и изменяет величину одного бита: если на входе О, то на выходе 1, и наоборот. Для его обозначения используется следующий символ.

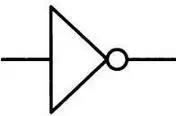
Поведение вентиля И-НЕ представлено в таблице. Рядом — символ, используемый для обозначения данного вентиля.